Abstract
BACKGROUND AND PURPOSE: The T2-FLAIR mismatch sign is a validated imaging sign of isocitrate dehydrogenase–mutant 1p/19q noncodeleted gliomas. It is identified by radiologists through visual inspection of preoperative MR imaging scans and has been shown to identify isocitrate dehydrogenase–mutant 1p/19q noncodeleted gliomas with a high positive predictive value. We have developed an approach to quantify the T2-FLAIR mismatch signature and use it to predict the molecular status of lower-grade gliomas.
MATERIALS AND METHODS: We used multiparametric MR imaging scans and segmentation labels of 108 preoperative lower-grade glioma tumors from The Cancer Imaging Archive. Clinical information and T2-FLAIR mismatch sign labels were obtained from supplementary material of relevant publications. We adopted an objective analytic approach to estimate this sign through a geographically weighted regression and used the residuals for each case to construct a probability density function (serving as a residual signature). These functions were then analyzed using an appropriate statistical framework.
RESULTS: We observed statistically significant (P value = .05) differences between the averages of residual signatures for an isocitrate dehydrogenase–mutant 1p/19q noncodeleted class of tumors versus other categories. Our classifier predicts these cases with area under the curve of 0.98 and high specificity and sensitivity. It also predicts the T2-FLAIR mismatch sign within these cases with an under the curve of 0.93.
CONCLUSIONS: On the basis of this retrospective study, we show that geographically weighted regression–based residual signatures are highly informative of the T2-FLAIR mismatch sign and can identify isocitrate dehydrogenase–mutation and 1p/19q codeletion status with high predictive power. The utility of the proposed quantification of the T2-FLAIR mismatch sign can be potentially validated through a prospective multi-institutional study.
ABBREVIATIONS:
- GWR
- geographically weighted regression
- IDH
- isocitrate dehydrogenase
- LGG
- lower-grade glioma
- probability density function
Diffuse gliomas are rare-but-life-threatening neoplasms characterized by infiltrative tumor growth in the brain. They have traditionally been classified according to phenotypic subtypes, including astrocytomas, oligodendrogliomas, and glioblastomas.1,2 The incidence of gliomas has steadily increased with time, with currently 5.9 cases per 100,000.3 Among diffuse gliomas, the World Health Organization characterizes low-grade gliomas as grade II tumors, while grade III are anaplastic tumors and grade IV are glioblastomas.4 However, research based on the The Cancer Genome Atlas often groups tumors from grades II and III together as lower-grade to distinguish them from the phenotypically distinct grade IV glioblastomas.5⇓-7
Recent genomic studies have resulted in lower-grade gliomas (LGGs) being categorized on the basis of molecular biomarkers that are associated with differing prognoses and responses to treatment.1,6 LGGs are currently classified by the presence/absence of a mutation in the isocitrate dehydrogenase (IDH)1/IDH2 genes, as well as the presence/absence of codeletion of the 1p and 19q chromosomes (1p/19q).1,4,6 IDH mutations are known to confer improved survival in patients with LGG and potentially better treatment outcomes.1,6 The presence of the 1p/19q codeletion also indicates better survival outcomes as well as increased sensitivity to specific forms of treatment.1,6
An imaging phenotype known as the T2-FLAIR mismatch sign in LGGs has drawn interest as a robust diagnostic tool to identify a specific molecular subtype of LGGs, namely IDH-mutant 1p/19q noncodeleted astrocytomas.6⇓-8 This sign is characterized by the presence of complete/near-complete hyperintense signal on T2 TSE (referred to as T2 from here on) and a relatively hypointense signal on T2-weighted FLAIR (referred to as FLAIR from here on) except for a hyperintense peripheral rim. The T2-FLAIR mismatch sign was initially reported by Patel et al6 to be a highly specific marker for IDH-mutant, noncodeleted gliomas with a positive predictive value of 100% in both the test and validation sets. These results have been validated by multiple research groups with high specificity,7,9⇓⇓⇓⇓-14 and the T2-FLAIR mismatch sign is now considered a useful and robust imaging sign.8 However, we emphasize that the 100% positive predictive value studies were all based on retrospective studies,6,7,9⇓⇓⇓⇓-14 and the results cannot be directly assumed for a general population. For example, Johnson et al12 found that T2-FLAIR mismatch elicits false-positives for IDH-mutant, noncodeleted astrocytomas in pediatric glioma cases. Additionally, as discussed in Foltyn et al,14 looser definitions of “mismatch” that do not require complete or near-complete hypointense T2 signal and a hyperintense peripheral rim on FLAIR may also elicit false-positives.
Analyses of distinct histopathologic and radiologic features of the brain have been conducted to better understand the physiologic context of the T2-FLAIR mismatch. For example, ADC values computed from diffusion-weighted images were shown to identify IDH-mutant noncodeleted LGGs with high specificity, capturing cases in which a T2-FLAIR mismatch was not apparent, in addition to those in which a mismatch was present.15 This study suggests that T2-FLAIR mismatch is also involved in the pathways that enable the IDH-mutated noncodeleted gliomas to exhibit increased ADC values compared with other subtypes.15 Aliotta et al15 added that the T2-FLAIR mismatch has substantially higher ADC values and lower relative CBV values compared with other IDH-mutant noncodeleted cases that do not have a mismatch. These values are considered well-known prognostic factors for glioma cases, and ADC has been implicated as a possible proxy for differences in tumor microenvironment.15 Therefore, although specific molecular pathway information must be investigated to better understand the mechanism for the T2-FLAIR mismatch, there is marked evidence that a mismatch emerges as a special case of IDH mutation and 1p19/q noncodeletion and confers possible tumor differences, which could have potential prognostic or predictive implications in the future. Our discussion of ADC here is to provide some background on the biologic motivations of our work, and we would like to emphasize that our proposed approach uses only T2 and FLAIR imaging sequences.
Although several studies analyzing the T2-FLAIR mismatch are available, to our knowledge, this is a first attempt to develop a statistical framework to detect the T2-FLAIR mismatch from MR images alone. We hypothesized that a statistical framework should be able to discriminate among different molecular subtypes of LGGs, including between IDH-mutant tumors with and without 1p/19q codeletion as well as the presence of a T2-FLAIR mismatch, even when the characteristic peripheral ring is not visible. Such a framework should allow the robust analysis of image characteristics that confer discriminative power that is not easily achieved by human reviewers.
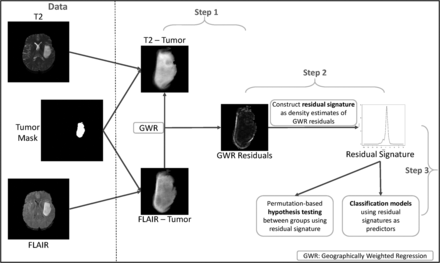
Our proposed statistical framework builds a quantification of the T2-FLAIR mismatch using patients’ MRIs to build a classifier for tumor subtypes on the basis of features extracted from the mismatch quantification. The proposed workflow of our approach is provided in Fig 1. We use a spatial analysis technique called geographically weighted regression (GWR)16 in combination with tools from geometric functional data analysis to quantify the mismatch between T2 and FLAIR. We refer to our quantification as a residual signature to differentiate it from T2-FLAIR mismatch. Using appropriate statistical frameworks (further details in the Materials and Methods section and the Online Supplemental Data), we devised permutation-based hypothesis tests to investigate differences among groups of residual signatures (eg, IDH-mutated versus IDH wild-type) and built classification models to predict the molecular status of the subjects. This framework of permutation tests and classification models has also been successfully used for the analysis of imaging data in the context of diabetic retinopathy.17,18
Workflow of our proposed approach. We obtained the tumor region from T2 and FLAIR scans using the tumor-segmentation mask. In step 1, we performed GWR with pixel values from the tumor region in T2 and FLAIR as the response and predictor, respectively. In step 2, a residual signature (ie, probability density function) was constructed using residuals from GWR. In step 3, we used residual signature–based features for hypothesis testing and classification models.
MATERIALS AND METHODS
Data
The multimodal MR imaging scans used in this study were obtained from The Cancer Imaging Archive19 and comprise baseline preoperative scans from 108 LGG tumors with segmentation labels generated by an automated algorithm and revised by an expert board-certified neuroradiologist.20,21 The tumor segmentation masks were matched across all MR imaging modalities. Clinical information including IDH status and the 1p/19q codeletion status was obtained from supplementary information provided with the 2016 pan-glioma article.22 The T2-FLAIR mismatch sign labels for these cases were used from the original publication,6 which was evaluated by 2 independent neuroradiologists. For these 108 subjects with LGGs, the sample composition for the molecular characteristics and mismatch signatures are shown in Table 1.
Sample composition for different molecular characteristics and mismatch signaturesa
Image Preprocessing
The voxel intensity values for the MR imaging scans are difficult to compare across subjects due to variation in scanner configurations. We preprocessed the scans to normalize the intensity values using a biologically motivated normalization technique called WhiteStripe (https://cran.r-project.org/web/packages/WhiteStripe/index.html).23 White Stripe normalization applies a z score transformation to the whole brain using parameters that are estimated from the distribution of normal-appearing white matter.23 It is shown to satisfy a set of 7 statistical principles for image normalization such as the following: 1) having a common interpretation across locations within the same tissue type, 2) being replicable, 3) preserving the rank of intensities, 4) having similar distributions for the same tissues of interest within and across patients, 5) not being influenced by biologic abnormality or population heterogeneity, 6) being minimally sensitive to noise and artifacts, and 7) not resulting in loss of information associated with pathology or other phenomena.23 This normalization is done for both T2 and FLAIR images. In our analysis, for each subject, we considered only 1 axial section of the MR imaging scan that had the largest connected component of tumor from the whole tumor region.
Geographically Weighted Regression
GWR is a spatial-analysis technique to study the spatially varying relationships between the response and covariates in a regression model.16 It is a statistical modeling approach similar to locally weighted regression used in curve-fitting and smoothing applications. The local regression parameters in a GWR are estimated by using subsets of data by appropriately weighting them (on the basis of proximity) with respect to the location at which the model is being estimated.
GWR Model.
We will explain the GWR model in the context of our analysis. Consider the T2 and FLAIR MR imaging scans for an axial section and the corresponding tumor segmentation mask. We perform GWR within the segmented tumor region with the pixel intensity values of T2 as the response and of FLAIR as predictors. For each tumor pixel, s = 1,...,n (where n is the total number of tumor pixels in the MR imaging), the GWR model is given as ys = βso + xsβs + εs, with ys and xs being the intensity values of the tumor pixel s from T2 and FLAIR MR imaging scans, respectively. Here, βso is the intercept, βs is the regression coefficient, and εs is the random error. The spatial location of a tumor pixel is identified by its corresponding grid coordinates from the axial section. We can compute the distance between any pair of tumor pixels as the Euclidean distance between the corresponding grid coordinates. These distances are used as input to a kernel function to compute weights that capture spatial dependence between the tumor pixels. For example, the weight corresponding to 2 tumor pixels in close proximity will be higher compared with the weight for pixels farther away from each other. These weights are then used to estimate the GWR model parameters at each tumor pixel s. Further details about the model formulation and estimation are provided in the Online Supplemental Data.
GWR Residuals.
As an illustration, we consider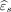 
to be the residual from the GWR model described above. Here, 
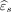can be interpreted as the amount of T2 pixel intensity not explained by the FLAIR pixel intensity through GWR. To quantitatively assess the mismatch between T2 and FLAIR images, we consider 
for all the tumor pixels s = 1,...,n and create a representation of the mismatch. We construct a probability density function (PDF) using these GWR residuals to quantify the mismatch. This PDF (referred to as the residual signature) acts as a surrogate for the mismatch and can be used for subsequent statistical analysis.
Probability Density Functions
The residual signature in our framework is an object of the space of PDFs. We wanted to have a metric (distance) that measures the dissimilarity between any 2 PDFs. There are multiple approaches to construct such a metric; however, they pose various computational challenges.24 We considered an equivalent representation of the PDFs via a square root transformation,25 which allows a simple computation of the distance between any 2 PDFs using the geometry of the space of square root transformations. This transformation also facilitates computation of an average (or mean) PDF, which provides efficient summarization and visualization, for the sample of PDFs. Details about the computation of the distance and average are provided in the Online Supplemental Data.
Permutation-Based Hypothesis Test.
We devised a permutation-based hypothesis test to investigate any differences in the average PDFs of the 2 groups (eg, IDH-mutated versus wild-type). Thus, we first computed the average PDFs of the 2 groups and used the distance between 2 average PDFs as the test statistic. We created the null distribution for the test statistic by randomly permuting the group labels between the subjects. A P value was constructed by comparing the test statistic with the null distribution (details in the Online Supplemental Data).
Classification.
Standard classification algorithms (eg, logistic regression, probit regression) can be used when the predictors belong to the Euclidean space. However, in our case, the data object corresponding to each subject is a PDF (ie, the residual signature). Hence, we used a geometric framework that maps each PDF to a vector of values via a principal component analysis for the sample of PDFs (details in the Online Supplemental Data). Using these Euclidean representations of PDFs (ie, the principal component scores), we constructed a probit regression model, a generalized linear model that models a binary categoric variable using numeric and/or categoric predictors.
RESULTS
For the 108 subjects with LGGs, we defined 6 different combinations of groups based on their molecular status and the T2-FLAIR mismatch sign.6 The 6 groupings and the corresponding sample size for each category are shown in Table 1. Three subjects were excluded due to missing data. The residual signature for each subject was constructed by computing the kernel density estimate from the GWR residuals.
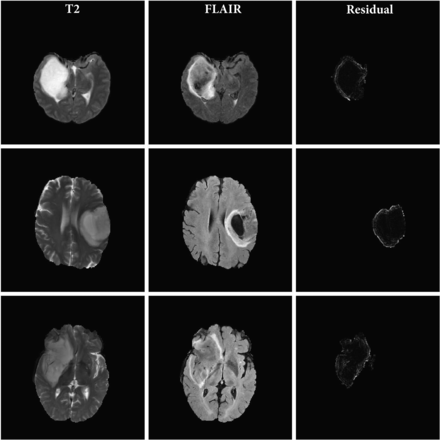
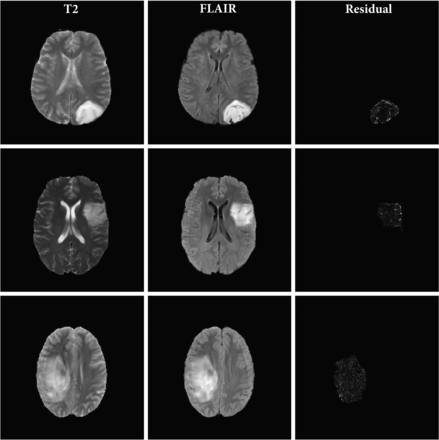
Figures 2 and 3 show the T2 TSE and FLAIR images and the pixel-wise GWR residual magnitudes from the tumor region for 3 sample cases with and without mismatch, respectively. We can see that the GWR residuals in Fig 2 clearly capture the hyperintense rim structure that is characteristic of a mismatch, whereas in Fig 3, there is no specific pattern to the GWR residuals but rather just a noisy distribution of pixel values over the tumor area. These images indicate that in cases with the mismatch, there is a clear difference in the axial rim along the boundary of the tumor between the T2 and FLAIR sequences.
T2 TSE and FLAIR MR images and the magnitude of the residual signatures corresponding to T2-FLAIR mismatch LGGs. Each row corresponds to an axial section from a patient tumor. The 3 columns represent the T2, FLAIR, and magnitude of the GWR residual for each tumor pixel, respectively.
T2 TSE and FLAIR MR images and the magnitude of the residual signatures corresponding to no-mismatch LGGs. Each row corresponds to an axial scan from a patient’s tumor. The 3 columns represent the T2, FLAIR, and magnitude of the GWR residual for each tumor pixel, respectively.
Hypothesis Test Results
For each grouping, we computed the group averages of the PDFs as described in the Materials and Methods section. These group-wise average PDFs are shown as a figure in the Online Supplemental Data for each of the 6 groupings (A)–(F). Differences in the group averages are visually evident (through the differences in the peaks and tails) for the groupings (B)–(F) but not for (A). We performed the permutation-based hypothesis test to evaluate these differences in the groups and compute P values as described in the Materials and Methods section. We considered 100,000 random permutations for each test, and the corresponding P values are presented in the second column of Table 2. We also present the false discovery rate–adjusted P values to account for multiple comparisons (ie, multiple hypotheses tests). From these results, we see that the average residual signature (or the average PDF) among the groups for the groupings (B)–(F) has a small P value (close to .05). This provides reasonable evidence against the null hypothesis that the average PDFs between the 2 groups are the same. This is in agreement with the visual differences in the average PDFs of these groupings (Online Supplemental Data).
P values (and adjusted P values) from permutation-based hypothesis tests to test for differences between the group averages of the PDFsa
Classification Results
We considered the residual signature for each subject as the predictor and built classification models (as described in the Materials and Methods section) with the corresponding group label as the response for each of the 6 groupings. We used a leave-one-out cross-validation approach for prediction, and the results are presented in Table 3. For example, we considered the grouping (A) for IDH status, ie, IDH-mutated and IDH wild-type, and obtained the vector representation of the PDFs by leaving 1 subject out and predicting the group label for the left-out subject. This process was repeated across all the subjects by leaving 1 subject out each time. We report the area under the curve, its Bonferroni-adjusted 95% confidence interval, sensitivity, and specificity. The confidence intervals are Wald-type, which are computed using the DeLong variance estimator26 using the pROC27 package in R statistical and computing software (http://www.r-project.org/). Using our residual signatures as predictors, we saw a strong predictive performance for the groupings (A)–(C) and (F). Specifically, our residual signatures have strong sensitivity and specificity for the 1p/19q codeletion status in IDH-mutant LGGs.
Classification results based on leave-one-out cross-validation approach for each of the 6 groupingsa
DISCUSSION
The T2-FLAIR mismatch sign is a well-validated indicator of IDH-mutant 1p/19q noncodeleted LGGs. In this study, we quantified the mismatch as a PDF constructed using the residuals from a locally (geographically) weighted regression of the T2 pixel intensities on the corresponding FLAIR image. Furthermore, we evaluated the utility of this residual signature in identifying various molecular subtypes of LGGs. We devised a permutation-based hypothesis test to detect significant differences among the average PDFs of groups on the basis of molecular subtypes of glioma and a classification algorithm to predict subtype labels of the tumor.
Figures 2 and 3 capture the hyperintense rim structure that is characteristic of the T2-FLAIR mismatch signature. The visually observed differences in rim intensity are summarized in a figure in the Online Supplemental Data; cases having the T2-FLAIR mismatch have wider tails in their average PDFs than those without. This could be indicative of the high magnitude of residuals coming from the tumor rim. Given the high specificity of the mismatch signature to the IDH-mutant 1p/19q noncodeleted class of gliomas, we compared the residual signature of these cases with other classes. Most interesting, we observed significant differences in the average profile of this class of gliomas compared with other subtypes, regardless of their mismatch labels. Results from the permutation-based hypothesis test agree with visual differences in mean signatures. Specifically, comparisons (B) and (C) indicate significant differences in mean residual profiles of the IDH-mutated 1p/19q noncodeleted class of tumors. This result combined with the comparison (F) about differences within this subclass with and without mismatch indicate the utility of our approach. Our GWR-based approach is able to learn subtle features from the images that are difficult to discern visually. These features could potentially serve as sensitive markers for the IDH-mutant noncodeleted subtype of gliomas. To validate this hypothesis, we devised a classification algorithm using Euclidean representations (ie, principal component scores) of the T2-FLAIR GWR residual signatures.
The features extracted from GWR residuals are highly predictive of major glioma subtypes. Our classifier identifies IDH-mutated 1p/19q noncodeleted cases with near certainty in comparisons (B) and (C), which is better than its performance in identifying the mismatch within these cases in comparisons (D) and (E). Our classification model has high sensitivity and specificity to discriminate the 1p/19q codeletion status in IDH-mutant LGGs. This observation supports the findings of Patel et al6 that report a 100% positive predictive value in predicting IDH-mutated astrocytomas by visual inspection in a retrospective study. Our work, however, builds on this result in several important ways. First, our results demonstrate that IDH-mutated 1p/19q codeletion status can be identified in gliomas from the residual signatures computed using GWR with high areas under the curve and specificity. Second, our work is not influenced by any of the inter- and intra-observer variability that is inherent in visual inspection of the mismatch sign from the MR images. Our framework is built on quantitative image analysis and rigorous statistical theory and provides a potentially powerful radiogenomic tool for identifying various molecular subtypes of gliomas. Our results indicate that radiomic features based on a T2-FLAIR mismatch are highly predictive of the IDH-mutant noncodeleted glioma subtype and provide a comprehensive quantitative alternative to the visually observed mismatch signature.
Furthermore, our statistical framework does not require advanced computing resources. The GWR model estimation is the only computationally intensive step in our framework, which, on average, took about 22.5 seconds per subject to execute. This time varies with the number of tumor pixels (ie, varying tumor sizes). Further details about the computation time are provided in the Online Supplemental Data. Software to implement our approach can be made available on reasonable request and with appropriate permissions from the University of Michigan.
CONCLUSIONS
Inspired by the value of the T2-FLAIR mismatch in identifying molecular subgroups of gliomas, we have developed a fully automated algorithm for quantifying the extent of mismatch between T2 and FLAIR scans, given tumor segmentation masks and extracted features from the T2-FLAIR residual signature that are strongly predictive of the glioma subtypes. We have shown that the residual signatures computed from performing GWR can be used to build classifiers that are potentially highly specific as well as sensitive to the IDH-mutant 1p/19q noncodeleted class of gliomas but need to be tested in a real-world environment through a prospective multi-institutional study. Visual identification of the T2-FLAIR mismatch sign is challenging due to its qualitative definition and readout, as well as the low sensitivity in identifying the IDH-mutant noncodeleted class of gliomas.14 Our approach builds highly accurate classifiers on the basis of statistically informed features of the T2-FLAIR mismatch and may be a useful tool in predicting the molecular subtypes in LGGs.
Footnotes
V. Ravikumar and E. Warner contributed equally to this work.
The content of this publication is solely the responsibility of the authors and does not represent the official views of the National Institutes of Health.
Disclosures: Shariq Mohammed—RELATED: Grant: National Institutes of Health.* Visweswaran Ravikumar—RELATED: Grant: National Institutes of Health–National Cancer Institute grants R37-CA214955, CCSG P30 CA046592, ACS RSG-16-005-01.* Elisa Warner—RELATED: Grant: National Institutes of Health/American Cancer Society, Comments: paid by the National Cancer Institute and American Cancer Society, respectively, to the University of Michigan, Ann Arbor.* Sohil Patel—UNRELATED: Grants/Grants Pending: National Institutes of Health, Comments: National Cancer Institute, award No. GI15673.* Spyridon Bakas—RELATED: Grant: National Institutes of Health, Comments: Research reported in this publication was partly supported by the National Cancer Institute and the National Institute of Neurological Disorders and Stroke of the National Institutes of Health under award numbers NCI:U01CA242871, NCI:U24CA189523, and NINDS:R01NS042645. Arvind Rao—RELATED: Grant: National Institutes of Health–National Cancer Institute, American Cancer Society*; UNRELATED: Consultancy: Voxel Analytics, LLC; Employment: University of Michigan, Ann Arbor; Payment for Lectures Including Service on Speakers Bureaus: Cambridge Healthtech Institute. Rajan Jain—UNRELATED: Royalties: Thieme. *Money paid to the institution.
S. Mohammed and A. Rao acknowledge support from the National Institutes of Health–National Cancer Institute grants R37-CA214955 and CCSG P30 CA046592, the University of Michigan Institutional Research Funds, and ACS RSG-16-005-01. S. Mohammed was partially supported by Precision Health at the University of Michigan. S.H. Patel was supported by the National Institutes of Health–National Cancer Institute grant GI15673. S. Bakas was supported by the National Institutes of Health–National Cancer Institute grants U01CA242871 and U24CA189523, and the National Institutes of Health–National Institute of Neurological Disorders and Stroke grant R01NS042645.
Indicates open access to non-subscribers at www.ajnr.org
References
- Received March 29, 2021.
- Accepted after revision September 3, 2021.
- © 2022 by American Journal of Neuroradiology
