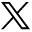Abstract
BACKGROUND AND PURPOSE: Measuring transmantle pressure, the instantaneous pressure difference between the lateral ventricles and the cranial subarachnoid space, by intracranial pressure sensors has limitations. The aim of this study was to compute transmantle pressure noninvasively with a novel nondimensional fluid mechanics model in volunteers and to identify differences related to age and aqueductal dimensions.
MATERIALS AND METHODS: Brain MR images including cardiac-gated 2D phase-contrast MR imaging and fast-spoiled gradient recalled imaging were obtained in 77 volunteers ranging in age from 25–92 years of age. Transmantle pressure was computed during the cardiac cycle with a fluid mechanics model from the measured aqueductal flow rate, stroke volume, aqueductal length and cross-sectional area, and heart rate. Peak pressures during caudal and rostral aqueductal flow were tabulated. The computed transmantle pressure, aqueductal dimensions, and stroke volume were estimated, and the differences due to sex and age were calculated and tested for significance.
RESULTS: Peak transmantle pressure was calculated with the nondimensional averaged 14.4 (SD, 6.5) Pa during caudal flow and 6.9 (SD, 2.8) Pa during rostral flow. It did not differ significantly between men and women or correlate significantly with heart rate. Peak transmantle pressure increased with age and correlated with aqueductal dimensions and stroke volume.
CONCLUSIONS: The nondimensional fluid mechanics model for computing transmantle pressure detected changes in pressure related to age and aqueductal dimensions. This novel methodology can be easily used to investigate the clinical relevance of the transmantle pressure in normal pressure hydrocephalus, pediatric communicating hydrocephalus, and other CSF disorders.
ABBREVIATIONS:
- FSPGR
- fast-spoiled gradient recalled
- PC
- phase-contrast
- VENC
- velocity encoding
Transmantle pressure, the instantaneous pressure difference between the lateral ventricles and the cranial subarachnoid space, drives cyclic CSF flow in and out of the ventricles through the cerebral aqueduct. The aqueductal flow velocities driven by transmantle pressure have clinical potential value in triaging patients with normal pressure hydrocephalus,1,2 investigating the pathogenesis of hydrocephalus,3 and understanding the effects of craniotomy (trephination)4,5 or lumbar puncture,6 and in other indications. Transmantle pressure can be measured using simultaneous readings from dual pressure sensors placed surgically in the cranial vault. However, there is a need to develop an accurate methodology to calculate it through nonintrusive methods. This represents a challenge because the transmantle pressure is very small. Results of direct measurements in both humans and animals typically show small differences or differences within the experimental error of measurement.7⇓⇓-10 Therefore, some prior studies have argued that these small changes of transmantle pressure could not be responsible for the development of hydrocephalus.9,10
Pressure drop is approximately proportional to the fluid acceleration, which increases in narrow channels such as the cerebral aqueduct. The pressure drop between the lateral ventricles and the subarachnoid space is then mainly due to that occurring along the aqueduct, which is the lengthiest narrow passage in the ventricular system.11 Therefore, noninvasive calculations of transmantle pressure typically focus on measuring the flow acceleration along the cerebral aqueduct.11⇓⇓-14 These noninvasive computational studies estimate small transmantle pressure values on the order of a few Pascals, consistent with those measured invasively. However, previously reported calculations of transmantle pressure were performed on a limited number of subjects, neglected relevant flow effects like convective acceleration, and/or relied on full computational fluid dynamics simulations, which are difficult to implement clinically.
The goal of this study was to compute transmantle pressure from noninvasive aqueductal flow measurements using a simplified nondimensional fluid mechanics model previously published by Sincomb et al,15 which accounts for the specific anatomic features of the aqueduct and relevant effects of local fluid acceleration, convective acceleration, and viscous forces. We applied this novel methodology to a group of volunteers to investigate differences related to age, sex, flow, and variations such as stroke volume, aqueductal length, and cross-sectional area on the transmantle pressure.
MATERIALS AND METHODS
Study Subjects
Subjects for this study were participants in a brain aging study funded by the LK Whittier Foundation (n = 48) and patients (n = 34) in a brain health and memory loss clinic and healthy student volunteers (n = 5). All subjects signed consent for enrollment in this institutional review board–approved study through Huntington Medical Research Institutes. Individuals with known neurologic or neurosurgical disorders were excluded. In the memory loss clinic group, individuals with a Clinical Dementia Rating of >0.5 of 5 were excluded.16 Written informed consent for inclusion in the study was obtained for all participants. All images were reviewed by a neuroradiologist to identify and exclude cases of acute or obstructive hydrocephalus and other abnormalities. Blood pressure and arterial pulse pressure were not recorded.
MR Imaging Acquisition
Imaging was performed with a 3T Signa scanner (software Version HD23; GE Healthcare) with an 8-channel head coil. The MR imaging included the routine localizer, axial, coronal, and sagittal T1- and T2-weighted images. Sequences obtained included a sagittal 3D inversion recovery fast-spoiled gradient recalled (FSPGR) sequence with the following parameters: TR/TE = 6.9/2.5 ms, TI = 600 ms, flip angle = 8°, acquisition voxels = 0.9 × 0.9 × 1.2 mm; and a single-shot gradient recalled-echo 2D phase-contrast (PC) sequence acquired perpendicular to the cerebral aqueduct, with the following parameters: TR/TE = 20/10 ms, velocity encoding (VENC) = 5–20 cm/s, flip angle = 20°, peripheral pulse gating with 30 retrospective cardiac phases, voxel size = 0.2 × 0.2 × 5.0 mm to 0.47 × 0.47 × 5.0 mm.
Flow Analysis
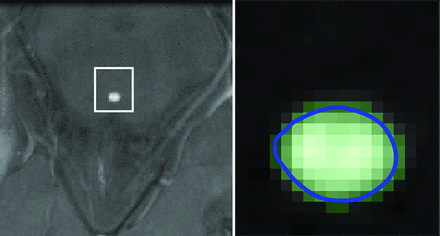
PC MR images were processed in Matlab (Version R2019a; MathWorks). The investigator placed a cursor on the aqueduct in the average-magnitude image. The program generated an optimal rectangular ROI around the cursor for the Otsu threshold algorithm and converted pixels in the ROI to a binary scale (graythresh). A boundary was computed separating the black and white pixels, and the cross-sectional area of the aqueduct was calculated automatically as the area within the boundary (bwboundaries) (Fig 1). Flow in each white pixel of the aqueductal area was calculated by linear magnitude–weighted conversion of phase to velocity and background correction.17,18 If the temporal velocity difference in a voxel was larger than 1.1 times the velocity encoding, antialiasing was performed.19 The flow rate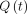 
, was computed by averaging the velocity magnitudes of all pixels within the aqueductal ROI and multiplying by the cross-sectional area. Caudal flow has a positive sign, and rostral flow, a negative sign.20 The stroke volume was computed as half the integral of the flow rate.2 Subjects with evident motion-related artifacts were excluded. In 1 subject imaged twice, inter-examination repeatability of the flow rate was calculated.
Axial PC MR imaging magnitude image (left) illustrating the aqueduct and optimal ROI window (white line) and corresponding binary image (right) from the Otsu algorithm (light green) displaying the boundary (blue line) automatically overlaid onto the magnitude image.
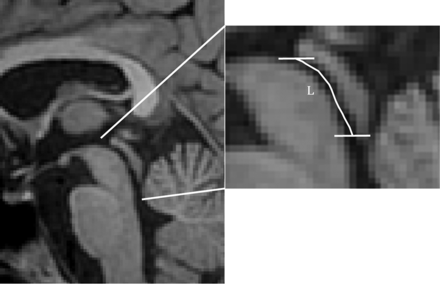
FSPGR images were used to segment the aqueduct semi-automatically using ITK-SNAP (Version 3.6.0; www.itksnap.org).21 The rostral and caudal ends of the aqueduct were identified manually as the point where the fluid lumen increased by 50%. The resulting 3D binary image stack was subsequently processed in Matlab. The geometric centroids of the aqueductal cross-sectional area were automatically identified in the axial plane of the 3D image stack, which was used along with the section spacing to compute the length of the aqueduct (Fig 2).
Sagittal FSPGR MR image (left) showing the aqueduct, third and fourth ventricles, and a collimated image (right). Enlarged MR image (right) shows the length of the aqueduct by means of a line connecting its centroid at each section (white line). The horizontal lines show the junction of the aqueduct with the third and fourth ventricles.
Transmantle Pressure Computation
The pressure difference between the third and fourth ventricles was calculated using the fully nondimensional computational fluid dynamics method previously described in Sincomb et al.15 The reader is referred to this publication for the details of the computational fluid dynamics model. The corresponding computer codes to calculate the transmantle pressure will be made available by the authors on request. One advantage of nondimensionalization is that it reduces the computational cost while retaining all important physical phenomena affecting the pressure variation including the local acceleration, convective acceleration, and viscous forces. In this respect, the model is superior in accuracy to 1-term formulas directly applicable to the PC MR image.22 The main input to the model included the aqueductal length, aqueductal cross-sectional area, flow rate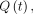 
stroke volume, and heart rate. The cross-sectional area of the aqueduct was assumed to be constant along the length of the aqueduct for this computation. Each variable was scaled with its corresponding characteristic value. The density and kinematic viscosity of CSF were assumed as 
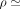103 kg/m3 and 
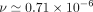m2/s, respectively. As mentioned previously, the resulting transmantle pressure is calculated as the pressure difference between the third and fourth ventricles, given as 
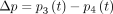, because the drop in pressure across the foramen of Monro and the median aperture is an order of magnitude smaller. This estimate of the transmantle pressure also neglects spatial pressure variations in the subarachnoid space because there the pressure is nearly uniform at any instant in time; thus, the spatial pressure differences never exceed a fraction of a Pascal as revealed in detailed computational fluid dynamics simulations of the entire cranial cavity.11 We, therefore, excluded any subject with MR imaging evidence of subarachnoid space obstruction.
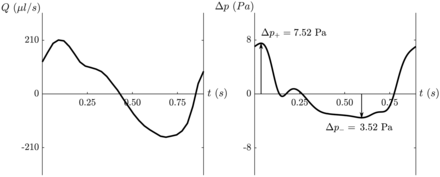
For all subjects, we computed the variation of transmantle pressure over a cardiac cycle (Fig 3). The variation of the transmantle pressure was then used to determine the peak positive transmantle pressure difference and negative transmantle pressure difference during caudal and rostral flow, respectively.
Plot of aqueductal flow (left) in a healthy 37-year-old man with an average heart rate of 67 beats per minute. Plot of the transmantle pressure (right) after entering variables into the nondimensional model15 and converting back to dimensional pressure (in Pascals). On the plot of transmantle pressure, the peak positive (ΔP+) and negative (Δp–) transmantle pressures are demonstrated by arrows representing peak pressures during caudal and rostral aqueductal flow, respectively.
Statistical Analysis
Differences in flow and anatomic and transmantle pressure values between men and women were tested by means of the Mann-Whitney U test. The Spearman rank correlation was used to assess the relationship between peak transmantle pressure values and aqueductal flow, age, heart rate, aqueductal length, and aqueductal area. These relationships were illustrated with scatterplots. Statistical significance was set as a P < .05.
RESULTS
Study Subjects
Of the 87 subjects, 9 subjects were excluded due to imaging artifacts such as motion. One subject with stroke volume >3 times the average was excluded as an outlier, which did not affect significant P values. The subjects for this study included 77 individuals, 28 men and 49 women, 25–92 years of age (average 69 [SD, 14] years) (Table 1). No subjects were excluded on the basis of review of MR images. Male and female subjects, on average, had similar ages and heart rates (Table 1).
Age, heart rate, aqueductal flow, and anatomic features and peak transmantle pressuresa
Flow Analysis
Eight subjects had high velocities that exceeded our VENC and thus benefited from antialiasing. The subject scanned twice for interexamination repeatability showed a difference in the estimated cross-sectional area of 5.6% and peak flow rates of 3.2% (Online Supplemental Data). In the 77 subjects, the cross-sectional area of the aqueduct averaged 3.15 (SD, 1.03) mm2 and differed significantly (P = .016) between women and men. The aqueductal length averaged 17.3 (SD, 2.8) mm, and the stroke volume averaged 40 (SD, 20) μl (Table 1).
Transmantle Pressure
During caudal aqueductal CSF flow, the peak positive transmantle pressure (higher pressure in the third ventricle than in fourth ventricle) in our participants averaged 14.44 (SD, 6.49) Pa and ranged from 1.63 to 31.77 Pa. During rostral aqueductal CSF flow, the negative transmantle pressure (higher pressure in the fourth ventricle than in the third) averaged 6.94 (SD, 2.82) Pa and ranged from 1.80 to 14.01 Pa. Differences between women and men in transmantle pressures were not significant (Table 1).
Statistical Analysis
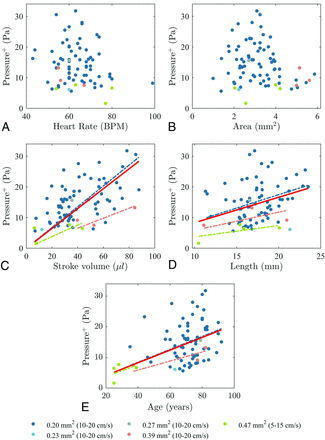
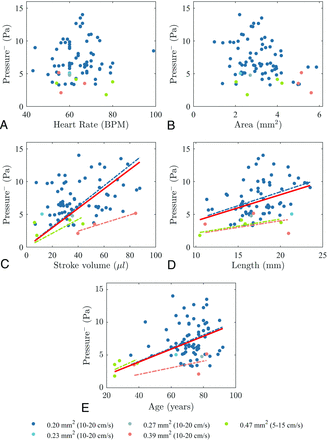
Peak transmantle pressure during caudal flow correlated significantly with age (ρ = 0.33, P = .004), aqueductal length (ρ = 0.33, P = .004), and stroke volume (ρ = 0.51, P <.001) (Table 2). It did not correlate with heart rate or aqueductal cross-sectional area, though the P value was near significance. Peak transmantle pressure during rostral flow correlated with the aqueductal cross-sectional area (ρ = −0.28, P = .013), aqueductal length (ρ = 0.37, P = .001), and stroke volume (ρ = 0.28, P = .014). It did not correlate with heart rate or age (Table 2). Scatterplots of peak positive and negative transmantle pressure with age, heart rate, aqueductal cross-sectional area, aqueductal length, and stroke volume are shown in Figs 4 and 5.
Peak transmantle pressure for all subjects and for subgroups of different voxel sizes (and VENC values) during caudal flow plotted against heart rate (A), aqueductal cross-sectional area (B), stroke volume (C), aqueductal length (D), and age (E), with trendlines including all subjects (red solid line) and subgroups of different voxel sizes with >1 subject. Transmantle pressure increases with stroke volume (ρ = 0.51, P <.001), aqueductal length (ρ = 0.33, P = .004), and age (ρ = 0.33, P = .004) for all subjects. Transmantle pressure also increases in each subgroup, but not significantly. BPM indicates beats per minute.
Peak transmantle pressure for all subjects and for subgroups of different voxel sizes (and VENC values) during rostral flow plotted against heart rate (A), aqueductal cross-sectional area (B), stroke volume (C), aqueductal length (D), and age (E), with trendlines including all subjects (red solid line) and subgroups of different voxel sizes with >1 subject. Transmantle pressure increases with stroke volume (ρ = 0.28, P = .014) and aqueductal length (ρ = 0.37, P = .001) for all subjects. The transmantle pressure tends to increase with age for the total group but does not reach significance (ρ = 0.18, P = .107). Transmantle pressure also increases in each subgroup, but not significantly. BPM indicates beats per minute.
Correlation of peak positive and negative transmantle pressure with age, heart rate, aqueductal area, stroke volume, and aqueductal length
DISCUSSION
We found that peak transmantle pressure during caudal flow increased with age from 1.62 Pa in one 25-year-old subject to 15.05 Pa in the 92-year-old subject. This finding indicates the relevance of age in the estimation of transmantle pressure. Aqueduct length and stroke volume correlated significantly with transmantle pressures in both the caudal and rostral direction. Peak transmantle pressure was inversely correlated with aqueductal cross-sectional area during caudal flow in the aqueduct, but not significantly during the typically less rapid rostral flow, suggesting that the viscous boundary layer effects must be taken into consideration when computing the transmantle pressure.
Peak transmantle pressure computed with the nondimensional computational model varied during the cardiac cycle from an average of 14.44 (SD, 6.49) Pa during caudal flow in the aqueduct to 6.94 (SD, 2.82) Pa during rostral flow. The computed peak transmantle pressure during caudal and rostral flow in this study is in general agreement with that in other computational studies23⇓-25 and also with measurements made with invasive methods in humans9,10 and in animals.7 In reports in which transmantle pressures were immeasurably small, the pressure sensors placed in the cranial vault had a resolution of 66 Pa, which is greater than the typical transmantle pressure in our study.8 To our knowledge, the peak pressures during both caudal and rostral flow have not been previously reported separately as we have done. This issue is important because the dynamics for caudal and rostral CSF flow (during systole and diastole, respectively) are distinct and may reflect influences of different system properties. The stroke volumes we measured in our volunteers also had a magnitude similar to those in previous studies including healthy younger and elderly subjects.18,26⇓-28
The study reported here is important because it shows that computational fluid mechanics methods based on a nondimensional formulation have sufficient precision to detect differences in transmantle pressure due to age or aqueductal dimensions, 2 important issues that have not been sufficiently evaluated to date. Our approach differs from that in previous studies related to transmantle pressure computation. For example, Sartoretti et al22 used the Bernoulli equation written in the form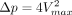 
to determine the pressure difference. This approach is only valid for steady flow, a condition that is not realized for the flow in the aqueduct. Linninger et al25 implemented a full computational fluid dynamics simulation that was computationally expensive. The computation used here can be performed with a readily available straightforward computer program in a few minutes and may be easily applied in the clinical setting.
Computation of transmantle pressure may be preferable to measurement of aqueductal velocity or stroke volume as an index of abnormal CSF dynamics. Computational studies of transmantle pressures are warranted in normal pressure hydrocephalus, pediatric communicating hydrocephalus, and other conditions with altered CSF dynamics. Owing to the viscoelastic nature of the brain parenchyma, even very small transmantle pressure may result in a gradual enlargement of the ventricles through the accumulation of small residual strain during months or years (tens of millions of cardiac cycles), while the mean intracranial pressure remains constant.29 This methodology to estimate transmantle pressure may have a role in studies of factors affecting ventricular morphology.30
This study has limitations. The health of the volunteers was not rigorously tested. However, acute or obstructive hydrocephalus and other abnormal brain conditions detectable by MR imaging that affect CSF dynamics were excluded by the neuroradiologist's review of MR images in each case. For PC MR imaging acquisition, variation of the VENC and in-plane resolution may have introduced some bias through velocity noise and partial volume effects respectively.31,32 However, groups with the same in-plane resolution showed the same trend for age and peak transmantle pressure. Neglecting longitudinal changes in the cross-sectional area of the aqueduct, for example at the ampulla, may have diminished the accuracy of the pressure computations. We did not study the effect of respiration on transmantle pressure, though it may be relevant.33 The test-retest precision of the pressure computation was not quantified, and it requires further study. Validation of the method also requires additional in vivo and in vitro experimentation.
CONCLUSIONS
Transmantle pressure computed with a recently described nondimensional fluid mechanics model revealed an increase of transmantle pressure with age. Aqueduct flow and anatomic dimensions affected the pressure computed. This computational method which incorporates relevant flow and anatomic features of the aqueduct may contribute to future studies of NPH, pediatric communicating hydrocephalus, and other CSF disorders.
ACKNOWLEDGMENTS
We wish to dedicate this work to Professor Juan C. Lasheras who passed away on February 1, 2021, after a short battle with cancer. Juan was the guide in our quest to bridge the fields of engineering and medicine. S.S. would like to acknowledge support from Bill & Melinda Gates Foundation. E.C.-H. would like to acknowledge Fundación Bancaria “la Caixa”.
Footnotes
This work was supported by the National Institute of Neurological Disorders and Stroke through contract No. 1R01NS120343-01. E.C.-H. acknowledges the partial financial support provided by Fundación Bancaria “la Caixa” (ID 100010434) through “la Caixa” fellowship (LCF/BQ/US12/10110011).
Disclosures: Stephanie J. Sincomb—RELATED: Grant: National Institutes of Health/National Institute of Neurological Diseases and Stroke, Comments: 1R01NS120343-01.* Kevin King—RELATED: Grant: Rudi Schulte Research Institute, Comments: Part of my time overseeing imaging for this project was related to research I was conducting for the Rudi Schulte Research Institute, whose primary goal was to understand biomarkers of normal pressure hydrocephalus.* and National Institutes of Health/National Institute of Neurological Diseases and Stroke, Comments: 1R01NS120343-01.* Matthew Borzage—RELATED: Grant: National Institutes of Health/National Institute of Neurological Diseases and Stroke, Comments: The Grant from the National Institutes of Health/National Institute of Neurological Diseases and Stroke that supports our study is 1R01NS120343-01. Antonio L. Sanchez—RELATED: Grant: National Institutes of Health/National Institute of Neurological Diseases and Stroke, Comments: 1R01NS120343-01.* Juan C. Lasheras—RELATED: Grant: National Institute for Neurological Diseases and Stroke, Comments: National Institutes of Health grant No. 1R01NS120343-01.* *Money paid to the institution.
References
- Received October 20, 2020.
- Accepted after revision May 27, 2021.
- © 2021 by American Journal of Neuroradiology
