Abstract
BACKGROUND AND PURPOSE: The intracranial volume is commonly used for correcting regional brain volume measurements for variations in head size. Accurate intracranial volume measurements are important because errors will be propagated to the corrected regional brain volume measurements, possibly leading to biased data or decreased power. Our aims were to describe a fully automatic SPM-based method for estimating the intracranial volume and to explore the practical implications of different methods for obtaining the intracranial volume and normalization methods on statistical power.
MATERIALS AND METHODS: We describe a method for calculating the intracranial volume that can use either T1-weighted or both T1- and T2-weighted MR images. The accuracy of the method was compared with manual measurements and automatic estimates by FreeSurfer and SPM-based methods. Sample size calculations on intracranial volume–corrected regional brain volumes with intracranial volume estimates from FreeSurfer, SPM, and our proposed method were used to explore the benefits of accurate intracranial volume estimates.
RESULTS: The proposed method for estimating the intracranial volume compared favorably with the other methods evaluated here, with mean and absolute differences in manual measurements of −0.1% and 2.2%, respectively, and an intraclass correlation coefficient of 0.97 when using T1-weighted images. Using both T1- and T2-weighted images for estimating the intracranial volume slightly improved the accuracy. Sample size calculations showed that both the accuracy of intracranial volume estimates and the method for correcting the regional volume measurements affected the sample size.
CONCLUSIONS: Accurate intracranial volume estimates are most important for ratio-corrected regional brain volumes, for which our proposed method can provide increased power in intracranial volume–corrected regional brain volume data.
ABBREVIATIONS:
- ARBM
- automatic reverse brain mask
- HUNT
- Nord-Trøndelag Health Study
- ICC
- intraclass correlation coefficient
- ICV
- intracranial volume
- RBM
- reverse brain mask
- SPM
- Statistical Parameteric Mapping
A large part of the variability in regional brain volume measurements can be explained by differences in head size because individuals with larger heads tend to have larger brain structures than people with smaller heads. Thus, regional brain volumes are usually normalized by some measure of the head size to reduce this variability. The most commonly used measure is intracranial volume (ICV),1 which is defined as the volume inside the cranium, including the brain, meninges, and CSF. The ICV is often preferred over the brain volume because it is a good measure of premorbid brain size.2
Manual delineation is considered the criterion standard for measuring ICV on MR images, but it is labor-intensive; therefore, a number of automatic methods have been developed. Two of the most popular are one by Buckner et al3 implemented in FreeSurfer (http://surfer.nmr.mgh.harvard.edu/) and another based on the Statistical Parameteric Mapping (SPM) program package (www.fil.ion.ucl.ac.uk/spm/software/spm8).
Several of the automatic methods for estimating the ICV report good accuracy, with volume estimates close to those of manual measurements.3,4 However, because the ICV is seldom used directly but instead is used for reducing the variability due to head size in other regional brain volume measurements, it may be more relevant to consider how the accuracy of the ICV estimates affects the normalized regional brain volumes. This detail is important because the method for estimating the ICV can change the outcome of statistics on ICV-normalized regional brain volumes. This difference was shown in a recent study that compared statistics on normalized hippocampal volumes by using ICV estimates from FreeSurfer and SPM.5
The method for normalizing the regional brain volumes with the ICV will affect how errors in the ICV measurements are propagated to the normalized volumes. Two of the most common normalization methods are the “ratio” method, which amounts to dividing the regional brain volumes by the ICV, and the “residual” method, which uses residuals from a linear regression between the volume of interest and the ICV,6 but other techniques are also used.1,7,8 Studies have shown that the ratio method is more sensitive to errors in ICV than the residual method.1,9
In this study, we describe a fully automatic SPM-based method for estimating the ICV, which improves on previous SPM-based methods in 2 important ways; First, there is no need to define an empiric threshold for estimating the ICV; and second, our method can estimate the ICV by using both T1- and T2-weighted images, which might be more accurate than using only T1-weighted images. We assessed the accuracy of our method against manually traced ICV measurements and ICV estimates from FreeSurfer and an accurate SPM-based method, called the “reverse brain mask” (RBM).4 To explore the practical implications of both methods for obtaining the ICV and the normalization method (residual-versus-ratio correction), we estimated the sample sizes needed to detect significant differences in ICV-normalized regional brain volumes between 2 groups with ICV estimates from FreeSurfer, the RBM method, and our proposed method.
Materials and Methods
Subjects
The MR images in this study were from The Nord-Trøndelag Health Study (HUNT Study), which is a collaboration between the HUNT Research Centre (Faculty of Medicine, Norwegian University of Science and Technology), the Nord-Trøndelag County Council, the Central Norway Health Authority, and the Norwegian Institute of Public Health. The MR images in the HUNT MR imaging cohort (n = 1006) represent subjects (n = 14,033) who participated in the 3 public health surveys in Nord-Trøndelag County (HUNT 1, 1985–1987; HUNT 2, 1995–1997; HUNT 3, 2006–2008) in Norway. MR imaging examinations were performed from 2007 to 2009. The mean age for the subjects was 59 ± 4.2 years (range, 50.5–66.8 years) at the time of scanning. Of the 1006 MR imaging datasets, 40 had to be discarded because of motion or image artifacts (n = 34), missing T2-weighted images (n = 5), and failed FreeSurfer processing (n = 1), leaving 966 for analysis.
This study was approved by the Regional Committee for Ethics in Medical Research (REK-Midt #2011/456). All participants gave written informed consent before participation.
Subjects Selected for Manual Segmentation.
Images from 30 healthy individuals (15 men) were selected for manual segmentation. To avoid biasing the sample toward any particular age, we divided the sample into 3 age groups, 50–55 years, 55–60 years, and 60–67 years, and randomly selected 5 men and 5 women from each age group. The mean age for the subjects selected for manual segmentation was 58 ± 4.4 years (range, 51–65 years).
Image Acquisition
Examinations were performed on a 1.5T Signa HDx MR imaging scanner (GE Healthcare, Milwaukee, Wisconsin) with an 8-channel head coil at Levanger Hospital, Nord-Trøndelag. T1-weighted 3D MPRAGE images were acquired sagittally by using the following parameters: TE = 4 ms, TR = 10 ms, flip angle = 10°, matrix size = 256 × 256, FOV = 240 × 240 mm, 166 sections of 1.2-mm thickness. T2-weighted images were acquired axially by using the following parameters: TE = 7.8 ms, TR = 95.3 ms, flip angle = 90°, matrix size = 512 × 512, FOV = 230 × 230 mm, 27 sections, 4-mm section thickness, 1-mm gap.
ICV Measurements
Manual Tracing.
ICV was traced on the T1-weighted images by a single rater (V.B.) by using the ITK-SNAP software (Version 2.2.0, www.itksnap.org),10 by drawing along the outer surface of the dura using the lowest point of the cerebellum as the most inferior point.11 There was no active exclusion of sinuses or large veins. The pituitary gland was excluded by drawing a straight line from the anterior-to-posterior upper pituitary stalk. Drawings were made on each section in the axial plane. Intrarater accuracy was assessed by re-segmenting 10 randomly selected images from the previously segmented data after at least 2 months.
Automatic Methods
Standard FreeSurfer Method.
We used FreeSurfer, Version 4.5.0. FreeSurfer differs from the other methods evaluated here in that it does not produce an ICV mask but estimates the ICV from the scaling factor of the affine transform of the anatomic images to the Talairach template.3 This scaling factor is approximately proportional to the ICV, and by linearly fitting the scaling factor from a set of images in which the ICV also has been determined by manual tracing, one can use the slope from the fit to estimate the ICV, yielding ICV estimates with an accuracy equivalent that of manual segmentation.3
Optimized FreeSurfer Method.
Differences in image quality or subject composition could render the default scaling factor in FreeSurfer suboptimal for our data. Therefore, we optimized the scaling factor to the manual ICV estimates in our dataset. We refer to these results as “optimized FreeSurfer.”
Reverse Brain Mask Method.
The reverse brain mask method4 uses the unified segmentation algorithm12 in SPM to derive a nonlinear transform from template space to the subject's native image space. An ICV mask based on the tissue probability maps in SPM is transformed to native space, and by using an empirically derived threshold, one can obtain an estimate of the ICV.4 The RBM method was implemented in SPM8 with an improved unified segmentation algorithm called “new segment”13 and default settings for nonuniformity correction (bias full width at half maximum = 60-mm cutoff, and bias regularization = 0.0001 “very light regularization”). The threshold on the ICV probability mask was determined by least-squares, minimizing the volume difference between the ICV mask and the manually traced ICV volumes.
Automatic Reverse Brain Mask Method.
The RBM method needs a threshold to calculate the ICV. This can be obtained empirically as in the original implementation4 or by optimization against a manually segmented dataset as in this work. Both methods have disadvantages, however, and we implemented an alternative SPM-based method that avoided the use of a threshold. This “automatic reverse brain mask method” (ARBM) uses a manually drawn ICV mask in template space, which is transformed to native space by using the nonlinear transform from the “new segment” in SPM and nearest neighbor interpolation, thus avoiding any need for a threshold. The ICV mask in template space was traced on the 1-mm3 T1-weighted Montreal Neurological Institute template by using the same segmentation protocol as described previously and the same rater (V.B.) used for the manual segmentation.
ICV Estimates by Using Multispectral Data
T2-weighted images provide better contrast between the dura and skull. Our implementation of the RBM and ARBM methods allows multispectral input to the segmentation algorithm, and by using both the T1- and T2-weighted images, a more accurate estimate of the ICV might be achieved. We made additional ICV estimates with both the RBM and ARBM methods, by using T1- and T2-weighted images as input, which we refer to as “RBM multi” and “ARBM multi.”
Assessing the Accuracy of ICV Estimates
The accuracy of the automatic ICV estimates relative to manual tracing was assessed by the accuracy of the volume estimates, by the overlap of the ICV masks, and by the agreement between the measurements as quantified by the intraclass correlation coefficient (ICC).
The accuracy of the volume estimates was quantified by the mean of the relative volume difference (RDIFF) and absolute volume difference (ADIFF), both expressed as percentages. These metrics capture slightly different aspects: RDIFF is sensitive to systematic differences in the ICV, but not random errors that may cancel out over the whole sample, while ADIFF is sensitive to random errors.
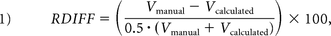
 We also quantified the overlap between the calculated ICV mask and the manually traced ICV mask by using the Dice coefficient,14 a unitless quantity ranging from 0 (no overlap) to 1 (perfect overlap). It is defined as the overlap between 2 binary images A and B, divided by the mean size of the 2 images.
We also quantified the overlap between the calculated ICV mask and the manually traced ICV mask by using the Dice coefficient,14 a unitless quantity ranging from 0 (no overlap) to 1 (perfect overlap). It is defined as the overlap between 2 binary images A and B, divided by the mean size of the 2 images.
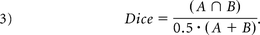 The Dice coefficient was only calculated for the SPM-based methods because FreeSurfer does not produce an explicit mask of the ICV.
The Dice coefficient was only calculated for the SPM-based methods because FreeSurfer does not produce an explicit mask of the ICV.
The agreement between the manual ICV measurements and the ICV estimates was quantified with a 2-way mixed single-measures ICC.15
Power Analysis
To explore how the different ICV estimates affect the statistical power in ICV-normalized regional brain volume measurements, we estimated the minimum sample size needed to detect a hypothetic volume difference between 2 groups by using the whole dataset of 966 subjects. We reported sample size estimates on 4 ICV measurements, the original FreeSurfer method, the optimized FreeSurfer method, and the 2 ARBM estimates. Results from the RBM method were omitted because they were almost identical to those of the ARBM method.
Regional brain volume measurements of subcortical gray matter structures, total cortical volume, and total white matter volume of the cerebrum and cerebellum were obtained with FreeSurfer (version 4.5.0) by using methods described in Fischl et al,16,17 and the volumes for the right and left hemispheres were added. The ICV was calculated with FreeSurfer, RBM, and ARBM methods as previously described. For the RBM method, we used the threshold optimized on the manually segmented images, and for the optimized FreeSurfer method, we used the scaling factor fitted to the manually segmented images.
ICV Normalized Volumes
The regional brain volumes were normalized with the ratio and residual methods. The ratio-corrected volumes were calculated as the ratio of the regional brain volume to the ICV. For the residual method, we expressed the ICV-corrected measurements as
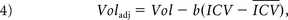 where Voladj is the ICV-corrected regional brain volume, Vol is the original uncorrected volume, b is slope from the linear regression of Vol on ICV, ICV is the intracranial volume for a particular subject, and I̅C̅V̅ is the mean ICV over all subjects. Note that ratio- and residual-corrected volumes must be interpreted differently18 and that the residual-corrected regional volumes have a zero correlation with the ICV, whereas the ratio-corrected volumes will usually correlate to some degree with the ICV.19
where Voladj is the ICV-corrected regional brain volume, Vol is the original uncorrected volume, b is slope from the linear regression of Vol on ICV, ICV is the intracranial volume for a particular subject, and I̅C̅V̅ is the mean ICV over all subjects. Note that ratio- and residual-corrected volumes must be interpreted differently18 and that the residual-corrected regional volumes have a zero correlation with the ICV, whereas the ratio-corrected volumes will usually correlate to some degree with the ICV.19
Estimating the Sample Size
For each regional brain volume measure, we calculated the minimum sample size required to detect a specified difference in the means between 2 groups when testing for a 2-sided difference with a power set to 0.8 and a type I error rate of 0.05. This calculation was performed for the raw volumes, the residual-, and ratio-corrected volumes.
We varied the effect size from 1% to 5% of the mean of the hippocampus volumes to determine how the sample size varied as a function of the effect size as an illustration of the general behavior. We also computed sample size estimates for all regional brain volume measurements for detecting a 2% difference from the mean, which amounts to approximately a “small effect size.”20 The effect was calculated on the uncorrected volumes as a percentage from the mean and transformed to the corrected volumes. The SD was calculated directly on the raw volumes and ICV-corrected volumes. For power calculations, we used the “power.t.test” part of the “stats” package in the R statistical computing software, Version 3.0.2 (http://www.r-project.org).
Results
Interrater Accuracy of Manual ICV Estimates
The intraclass correlation (2-way random, absolute agreement, single measures) was 0.99, indicating good agreement between the 2 manual segmentations.
Accuracy of ICV Estimates
The accuracy of the automatic ICV estimates compared with manual delineation is summarized in Table 1. (See On-line Table 1 for mean ICV values for each method.) The FreeSurfer measurements were the least accurate in terms of relative agreement, absolute agreement, and ICC. All ICV estimates by FreeSurfer were lower than the manual measurements, with a mean underestimate of 111 mL. The SDs in the volume differences were also the largest. The optimized FreeSurfer estimates were considerably better than the standard FreeSurfer estimates as seen by the mean and absolute mean of the volume differences, but the SD of the difference was still among the highest. The RBM and RBM multi methods had the lowest absolute mean differences. Table 1 also shows that the multispectral RBM method, by using both T1- and T2-weighted images, was slightly more accurate than the RBM method by using only T1-weighted images. The ARBM method performed in a manner comparable with the RBM method, but the absolute mean difference was slightly larger for the ARBM and ARBM multi methods compared with the RBM counterparts. The Dice and ICC values were very similar for the RBM and ARBM methods but also indicated a slightly better agreement when using multispectral data.
Accuracy of the automatic methods for estimating ICV compared with manual delineationa
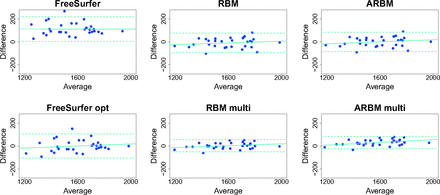
There was good agreement between the automatic methods and manual segmentation (Fig 1). The linear fit between the difference and average had a slightly positive slope for all methods except for the standard FreeSurfer ICV estimates (Fig 1) but was nonsignificant (all P > .14, r2 < 0.08) except for the ARBM multi method, in which the difference and average correlated significantly (P = .03, r2 = 0.15). This result indicates that the errors increased with increasing ICV. A potential consequence of such a biased error could be that a sex-related bias was introduced in the ICV estimates because men, on average, have a larger ICV than women. We did not, however, find significant differences between men and women in the errors of the ICV estimates (all P > .1; t < 1.7).
Bland-Altman plots show the ICV difference (manual-automatic) plotted against the mean of the 2 measurements. Units are in milliliters. The dotted horizontal lines are 2 SDs above and below the mean, and the solid line is the best-fit line from the regression of the difference on the mean.
The use of T1 and T2 images as input improved the accuracy of the RBM method. Table 1 shows that all accuracy metrics are improved for RBM multi over RBM. For the ARBM multi method, the benefits of using multispectral data are less evident. Although the ARBM multi method improves the ICC, Dice overlap, and SD of the volume differences over the ARBM method, the ARBM multi method underestimates, on average, the ICV by 1.9%, compared with only −0.1% for the ARBM method (Table 1).
Sample Size Calculations
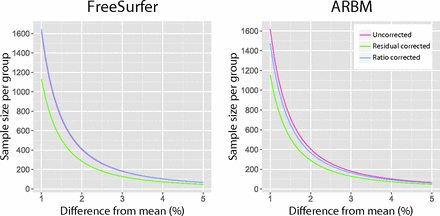
Figure 2 shows how the sample size varied over a range of effect sizes for hippocampal volumes normalized with ICV estimates from the FreeSurfer and ARBM methods. The differences in the required sample sizes were most pronounced for small effect sizes, whereas for larger effect sizes, the differences between both ICV estimates and correction methods diminished. Figure 2 also shows that in terms of increasing power, the residual correction was more effective than the ratio correction.
Effect size in percentage difference from the mean plotted against the sample size per group for uncorrected hippocampal volumes and ICV-corrected hippocampal volumes by using FreeSurfer and ARBM ICV estimates.
The minimum sample sizes per group required to detect a 2% difference in regional brain volume measurements are shown in Table 2. Compared with the uncorrected volume measurements, both the ratio and residual corrections reduced the required sample size considerably. With residual correction, the differences in the estimated sample size were small and generally in favor of the FreeSurfer methods. The largest difference was for normalized caudate volumes, in which the ICV derived from the ARBM method would require 32 more subjects per group than using the ICV from FreeSurfer. With ratio correction, the differences were larger, as expected. Comparing the standard FreeSurfer estimates with the ARBM estimate showed that the ARBM estimate reduced the sample size considerably for some structures. For the hippocampus volumes, sample size was reduced by 44, and for nucleus accumbens, by 52 subjects per group when using the ARBM ICV estimate compared with the FreeSurfer ICV values. The difference was even larger with the ARBM multi method, with a reduction in the sample size of 51 and 61 per group for the hippocampus and nucleus accumbens, respectively.
Required sample size per group for detecting a 2% difference in raw and ICV-normalized regional brain volumes between 2 groups, with a power of 0.8 and a type I error rate of 0.05
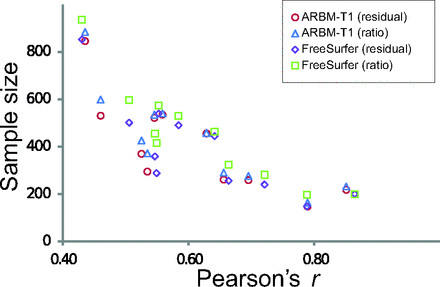
There was considerable variation in the required sample size for the different regional volume measurements (Table 2), with cerebral cortex and cerebral white matter volumes requiring the lowest sample sizes, whereas nucleus accumbens measurements required a sample of >800 subjects to reach sufficient power. We found that the sample size was associated with the strength of the correlation between the regional volume measurements and the ICV. This result is expected for the ratio-normalized volumes because there is a linear dependence between the variance of ratio-corrected volumes and the correlation between the ICV and raw volume.19 However, a similar relationship was also found for the residual-corrected volumes. The association between the Pearson correlation coefficient and sample size estimates for both the residual- and ratio-correction methods is plotted in Fig 3. (See On-line Table 2 for correlation coefficients between the regional brain volumes and the different ICV estimates.)
The relationship between sample size estimates for detecting a 2% difference from the mean and Pearson's r between uncorrected regional volumes and ICV estimates.
Discussion
Accuracy of the Automated Methods versus Manual Segmentation
The automatic methods for estimating the ICV, which we evaluated, produced ICV estimates that closely matched those of manual segmentation. The ICV FreeSurfer estimates had a bias that was larger than the other methods, and FreeSurfer consistently underestimated the ICV. A possible cause is that the default scaling factor in FreeSurfer is not optimal for the present study, or that differences between the segmentation protocol for the images on which the scaling factor was optimized and that of the present study could account for the bias.
Optimizing the FreeSurfer scaling factor improved the ICV estimates. A drawback is that one must have a sufficiently large set of images with manually derived ICV measurements to compute an optimized scale factor. Future studies could determine whether the variation in the optimal scaling parameter is primarily determined by the scanner parameters or by the study population.
The RBM method was the most accurate for estimating the ICV. We also found that in comparison with the original implementation of the RBM method, the “new segment” algorithm in SPM improved the accuracy of the RBM method. (See On-line Table 3 for a summary of the accuracy of the original RBM method.) A disadvantage of the RBM method, however, is that one must set an empiric threshold for calculating the ICV. Therefore, the accuracy of the RBM method is dependent on the threshold. This dependency is illustrated in On-line Table 3 showing the accuracy of the RBM method with the optimized threshold and with the threshold recommended by the authors of the RBM method.4 Using the nonoptimized threshold renders the RBM method less accurate than the ARBM method. We also found that a visual determination of the threshold was difficult because it varied among different raters. Optimizing the threshold against the manual segmentation result avoided this problem but is impractical in many instances because it necessitates manual measurements.
The ARBM method attempts to alleviate the drawback of using a threshold. An ICV mask must still be drawn in template space, but it needs to be done only once. The ARBM approach was, however, less accurate than the RBM method but more accurate than the FreeSurfer methods. The ICV estimates with the ARBM method may be robust over different field strengths, similar to those with the RBM method,4 because the 2 methods only differ in how the brain masks are thresholded.
Multispectral input clearly improved the accuracy of the RBM method, suggesting that the transformation from template space to native space is more accurate when using T1 and T2 images as input compared with using only T1 images. For the ARBM method, however, multispectral input resulted in a slight underestimation of the ICV. This discrepancy in accuracy between these methods can appear puzzling because they rely on the same transformation from template space to native space. The underlying cause is that the multispectral segmentation, on average, generates a slightly smaller volume in native space than the segmentation based on T1 images only. The bias is adjusted during the optimization of the threshold in the RBM method because the optimized threshold for RBM multi is 0.29 compared with 0.34 for the RBM method (a lower threshold results in a larger ICV mask). For the ARBM method, the ICV is fully determined by the transformation to native space; therefore, there is an increase in the mean volume difference for the ARBM multi method. The bias in the ARBM multi estimates is mainly a concern when using ratio correction. For residual correction, the ARBM multi method would still be preferable over the ARBM method because the multispectral segmentation reduces the variance in the volume estimates compared with the T1-only ARBM. This outcome is reflected in the slight decrease in sample size estimates for the ARBM multi method over the ARBM method (Table 2).
Sample Size Estimates
The ICV is often used for correcting variations in regional brain volume measurements due to differences in head size. Several studies have compared the accuracy of various ICV-estimation methods,3,4,21,22 but surprisingly few have examined the practical benefits of an accurate ICV measurement. Naively, one would expect that accurate ICV estimates would increase the statistical power of ICV-corrected regional volume measurements. Our results demonstrate that not only the choice of ICV estimate, but also the method of ICV correction can affect the statistical power. We found that residual correction resulted in only minor differences between the FreeSurfer and ARBM methods (Table 2). In fact, the FreeSurfer ICV correction generally required a smaller sample size than the ARBM-corrected volumes. This is surprising considering that the ARBM method had higher accuracy than FreeSurfer compared with manual segmentation (Table 1). However, the differences in the required sample sizes for the volume estimates can largely be explained by the strength of the correlation between the ICV and the volume measurements (Fig 3).
We found that accurate ICV estimates were more crucial for the ratio-corrected volumes, a finding that is in agreement with previous studies,9,19 and that the ratio-correction method, unlike the residual-correction method, requires absolute agreement in the ICV estimates. When using ratio correction, we found that the more accurate ARBM ICV estimates can provide increased power compared with the FreeSurfer ICV estimates. For example, to detect a 2% difference in the hippocampus volumes requires 44 fewer subjects per group when using ARBM ICV estimates compared with FreeSurfer ICV estimates. However, the difference in the required sample size becomes smaller for larger effects (Fig 2); for medium-sized or larger effects, there are only minor differences among the methods we evaluated.
Conclusions
In this article, we described an SPM-based method for calculating the ICV, which compared favorably against other available methods. Sample size estimates showed that ICV estimates from the ARBM method could increase the statistical power in ICV-corrected regional brain volume data compared with using ICV estimates from FreeSurfer, but only when using ratio correction and for small effect sizes. For detecting larger effects or when using residual correction, the choice of method for estimating the ICV became less critical. The ARBM method can serve as a robust and efficient method for obtaining accurate ICV estimates in large datasets and in datasets in which application of FreeSurfer or other software is not possible or needed. The Matlab (MathWorks, Natick, Massachusetts) source code for the ARBM method can be obtained from the corresponding author.
Acknowledgments
The authors thank Lars Jacob Stovner (Norwegian University of Science and Technology) and the HUNT administration for organizing and the MR imaging technologists at the Department of Radiology at Levanger Hospital for collecting the HUNT MR imaging data.
Footnotes
T.I.H. and V.B. contributed equally (shared first authorship).
This study was funded by the Norwegian Ministry of Education and Research.
Indicates open access to non-subscribers at www.ajnr.org
References
- Received September 29, 2014.
- Accepted after revision January 28, 2015.
- © 2015 by American Journal of Neuroradiology