Saccular Aneurysms on Straight and Curved Vessels Are Subject to Different Hemodynamics: Implications of Intravascular Stenting

In Vitro Flow Visualization Experiment

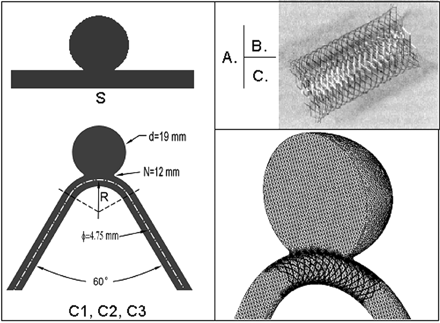
Two identical groups of elastomer aneurysm models, nonstented (control group) and stented (treatment group), with 4 different curvatures each (0 mm⁻¹ straight vessel, S; 0.04 ± 0.01 mm⁻¹, C1; 0.08 ± 0.01 mm⁻¹, C2; and 0.1 ± 0.01 mm⁻¹, C3) were created⁷ and used for in vitro flow visualization. This curvature range covers that typical of the rabbit elastase aneurysm model, based on models created at our center. Except for the parent vessel curvature, all geometric parameters (aneurysm diameter, neck size, vessel diameter, and angle of feeding and distal straight segments) remained constant (Fig 1A). Parent vessel curvature was defined as C = 1/R, R being the radius of the curvature of the vessel centerline in which the aneurysm was located. A self-expanding stent (5 × 40 mm; Wallstent, Boston Scientific, Natick, Mass) (Fig 1B) was deployed across the aneurysm neck in each of the 4 models in the treatment group.

• Download figure
• Open in new tab
• Download powerpoint

Fig 1.

Aneurysm model geometry. A, Sidewall aneurysm on a straight vessel (S) and aneurysms on curved vessels with different curvatures (C1–C3). Curvature is defined as C = 1/R, where R is the radius of curvature of the parent vessel. N indicates neck size; d, aneurysm diameter; φ, vessel diameter. B, Stent used in the flow experiment and mimicked in the CFD simulations (5 × 40 mm Wallstent). C, Computational mesh in a stented aneurysm model used for CFD analysis.

The working fluid for the in vitro flow models was a 60/40 mixture of glycerin and water (attenuation, 1.157 g/cm³; viscosity, 15.2 cP [1 cP = 0.001 Pa s]). A flow loop was set up as previously reported,⁷ except that a height-adjusted tank was used to achieve steady flow. The flow rate was 375 mL/min; the corresponding Reynolds number (Re) was 128. The Dean number, defined as {(ΦC/4)^1/2Re}, where Φ is the diameter of the vessel lumen and C is the vessel curvature, ranged from 28–44 for the curved vessel models in our experiment. These values (thus the curvatures) were within the typical range found in human cerebral arteries (10–200).⁸

An optical dye (diluted stamp refill ink, Stockwell, Package Design Stockwell, Wesborough, Mass) was manually injected (6 mL of dye; injection rate, ∼6 mL/s) near the aneurysm entrance to trace flow passing through the aneurysm. The models were oriented superiorly and posteriorly relative to respective parent vessels to examine the influence of orientation and possible gravity effect⁷ on flow visualization. No significant changes were found between these 2 orientations, indicating negligible gravity effect with the optical dye. The flow in each orientation was recorded 3 times by a digital camera in a particle image velocimetry system (proVISION system, Integrated Design Tools, Tallahassee, Fla). The output resolution of the camera was 1360 × 1024 pixels. The recording frequency was 12 Hz; total recording time was approximately 15 seconds per acquisition.

Time-Intensity Curve Analysis and Stasis Index Calculation

To quantitatively characterize aneurysmal flow obtained from each acquisition of the in vitro flow image series, a time-intensity curve (TIC) was calculated. The stasis index (SI) was defined as the half-peak width of the TICs and was measured in seconds. The SI intuitively indicates the duration that dye remained in the region of interest.

CFD Simulations

CFD analysis was performed on a series of aneurysm models similar to those used in the flow-visualization experiment and under the same flow conditions as in that experiment. The vessel curvature was 0 mm⁻¹ (S), 0.03 mm⁻¹ (C1), 0.07 mm⁻¹ (C2), and 0.11 mm⁻¹ (C3). A stent mimicking the Wallstent used in the flow experiment was simulated with the aid of computer-assisted design software (ProEngineering, PTC, Needham, Mass) (Fig 1C).

A steady-state flow condition was applied at the model inlet. Assumptions of Newtonian fluid, incompressible and laminar flow, and rigid wall were adopted. The CFD simulations were performed by using a commercial finite volume code (STARCD, Adapco, Melville, NY). Each stented model consisted of approximately 2.4 million tetrahedral meshes, and each nonstented model consisted of approximately 0.6 million tetrahedral meshes created by a software package (ICEM CFD, Ansys, Canonsburg, Pa) to achieve a stable solution. Mesh refinement tests were performed to achieve grid-independent simulation results. The CFD simulations provided 3D flow fields for each untreated and stented model.

Most CFD simulations were performed at the experimental flow condition of Re = 128. To evaluate how stent placement might affect wall shear stress (WSS) under a physiologically relevant flow condition, we also performed CFD simulations under higher flow (Re = 490), which matched the peak flow rate of a pulsatile flow at a patient’s basilar artery measured with phase-contrast MR imaging (private communication, August 2002, University of Illinois Research Group, Chicago, Ill). Cerebral artery flow usually does not exceed an upper limit of Re = 600–700,⁹ and Re values of 100, 400, and 700 have been used in a previous study.¹⁰

Hemodynamic Parameter Quantification from CFD Simulations

From the CFD flow field simulations, several hemodynamic parameters were calculated, including inflow momentum, WSS distribution, and impact zone. “Inflow region” was defined as the region at the interface between the aneurysm orifice and the parent vessel where flow velocity vectors pointed into the aneurysm. The “inflow momentum” was then calculated in the inflow region for each model. The WSS was calculated from the flow velocity gradient near the vessel wall by using the Newtonian fluid assumption. To quantify the influence of flow impingement at the distal neck of the aneurysm wall, we defined the “impact zone” as the area of the aneurysm wall where the WSS was elevated to >20 dynes/cm² for each model.¹¹

Flow Characteristics in Straight- and Curved-Vessel Aneurysm Models

There was a fundamental difference in flow mechanisms between the straight- and curved-vessel models. In the sidewall model, flow in the parent vessel was tangential to the aneurysm orifice. Its viscous force dragged a layer of fluid in the aneurysm to move along with it, resulting in a vortex in the aneurysm because of both the viscous shear force and confinement in the pouch. Being viscous shear-driven, the aneurysmal flow was relatively weak and sluggish.

In curved-vessel models, the aneurysm cavity was located along the inertial path of flow in the parent vessel. Inertial force drove flow into the aneurysm cavity. As curvature increased, the inertia-driven flow intensified and quickly dominated the aneurysmal flow field. These 2 distinct mechanisms are referred to as “shear-driven flow” and “inertia-driven” flow.

The 2 mechanisms brought about a significant difference in the strength of aneurysm flow. As vessel curvature increased from zero (straight model), inflow momentum drastically increased by several orders of magnitude (Fig 2; numbers above data points represent momentum for untreated models). From this result, we inferred that inertia-driven aneurysmal flow produced an inflow that was 10³–10⁴ times stronger than shear-driven flow.

• Download figure
• Open in new tab
• Download powerpoint

Fig 2.

Inflow momentum as a function of vessel curvature (zero curvature corresponds to the sidewall aneurysm) from CFD simulation (Re = 128). Inflow momentum is calculated at the interface between the aneurysm orifice and parent vessel. The values for both untreated and stented models are calculated, but only the untreated models are labeled with values to show the difference between the straight vessel model (S) and the curved vessel (C) models.

Flow Modification Induced by Stent Placement

The shear-driven and inertia-driven flow mechanisms led to very different results after stent placement across the aneurysm orifice, as demonstrated by CFD and experiments:

Stent Placement Disrupted the Vortex Flow Pattern in the Sidewall Model but Not in Curved Aneurysm Models.

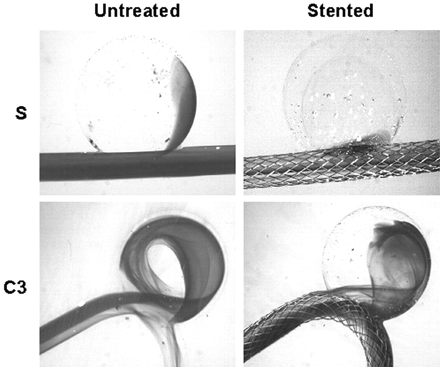
In the sidewall model (Figs 3 and 4), the stent struts broke up the developing shear layer into small wells through which flow sieved (contour plot in Fig 3 insert). The shear-driven inflow that ordinarily entered from the distal neck was redistributed across the orifice, and consequently, the counterclockwise aneurysmal vortex was disrupted by the stent. In contrast, in curved models, stent struts did not disrupt the overall inertia-driven inflow. Although the aneurysmal vortex was weakened by the stent placement, the counterclockwise vortex flow pattern remained nevertheless (Figs 3 and 4). Increasing vessel curvature among different curved models was associated with a stronger inflow jet and, hence, a stronger vortex with or without the stent.

• Download figure
• Open in new tab
• Download powerpoint

Fig 3.

CFD simulation (3D) of aneurysmal flow in the straight vessel model (S) and one of the curved vessel models (C3) (Re = 128). Plotted are 2-dimensional velocity fields in the center plane. Insert reveals flow sieving through the stent struts in the straight vessel model. Shown is the vertical velocity magnitude contour at the aneurysm–parent vessel interface.

• Download figure
• Open in new tab
• Download powerpoint

Fig 4.

Dye visualization of the straight vessel model (S) and one of the curved vessel models (C3). The pictures are selected from the third image after the first appearance of dye in the aneurysm sac to represent the wash-in status.

Stent Placement Significantly Increased Flow Stagnancy in the Sidewall Models but Not in High-Curvature Aneurysm Models.

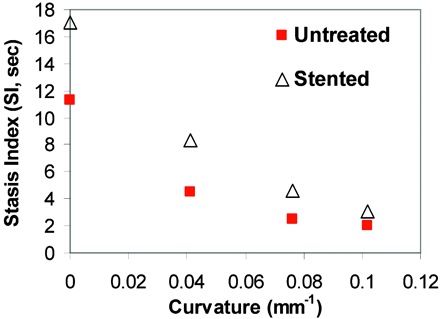
Although stent placement increased flow stasis for each model, this increase diminished significantly with increasing vessel curvature (Fig 5). The increase in SI, measured in seconds, for various models, is given in the Table.

• Download figure
• Open in new tab
• Download powerpoint

Fig 5.

SI before and after stent placement as a function of vessel curvature for each model (S, straight; C, curved vessel) in the dye visualization experiment. As the curvature increases, SI decreases. Stent placement increases SI, but the increment is smaller in larger curvature models.

View this table:

• View inline
• View popup

Effect of stenting on flow in sidewall (S) and curved (C) aneurysm models

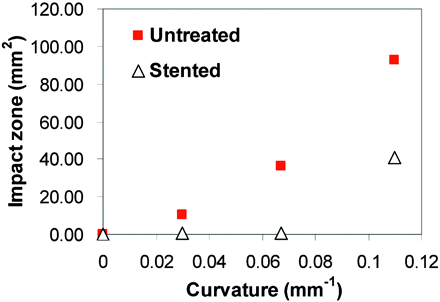
Stent Placement Reduced Impact Zone Under High Flow in All Aneurysm Models.

Under the low-flow condition (Re = 128), the size of the impact zone at the distal wall did not show appreciable changes with curvature or stent placement. However, under the more physiologic high-flow condition (Re = 490), WSS levels and impact zone size experienced significant changes due to vessel curvature change or stent placement (Fig 6).

• Download figure
• Open in new tab
• Download powerpoint

Fig 6.

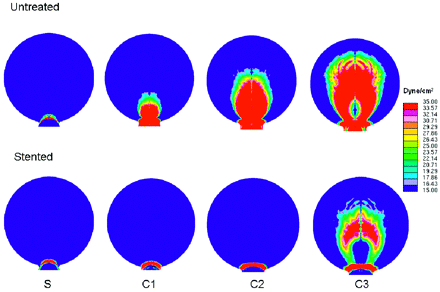
WSS distribution at the distal aneurysm wall and distal vessel wall in straight (S) and curved (C) models before and after stent placement, calculated from CFD simulation (Re = 490). Color scale represents WSS values from <15 dynes/cm² (deep blue) to >35 dynes/cm² (bright red). The impact zone is defined as the area where WSS is >20 dyne/cm², a value considered the upper limit for normal physiologic WSS.

The size of the impact zone (WSS, >20 dynes/cm²) on the wall was calculated and plotted against vessel curvatures (Fig 7). The impact zone was almost negligible for the untreated sidewall model but increased markedly with increasing curvature. Stent placement led to a dramatic reduction in the impact zone for all models: 61% for model S, 96% for model C1, 98% for C2, and 56% for C3 (listed in the Table). The percentage reduction of the impact zone in C3 (highest curvature) was lower than that in other models because the strong bend in the vessel rendered the stent to be less effective as a conduit for the flow in the parent vessel. As such, the jet shot in, resulting in impingement away from the neck region.

• Download figure
• Open in new tab
• Download powerpoint

Fig 7.

Impact zone for untreated and stented cases at various vessel curvatures, calculated from CFD simulation (Re = 490). The stent disturbs more impinging flow to decrease the impact zone at the moderately curved vessel, but the stent effect diminishes at the highly curved vessel.

Diminished Potential of Stent Placement for Thrombotic Occlusion of Aneurysms on Curves and Bifurcations

Our results have shown that the stent-induced flow reduction diminished with increasing vessel curvature. In the sidewall model, shear-driven flow is already considerably more sluggish than the inertia-driven flow in aneurysms on curves, even before stent placement. Hence, a porous stent could easily disrupt the aneurysmal vortex and create stasis in the canine aneurysm (as reported in numerous descriptions of successful thrombotic occlusion of sidewall aneurysm models).^3,4 In our curved models, however, the aneurysmal vortex flow pattern remained despite stent placement. Furthermore, as vessel curvature increased, stent-induced flow stagnancy decreased, with the highest flow reduction experienced in the sidewall model. Thus, the potential for stent-induced thrombotic occlusion was diminished for aneurysms on curves. The same can be expected from bifurcation aneurysms because the flow in these aneurysms is also inertia-driven.

More Protective Roles of Stents in Aneurysms on Curves or at Bifurcations

We found that Wallstent placement in curved-vessel aneurysm models drastically reduced inflow momentum, WSS, and impact zone size at the distal wall. Thus, we submit that stent placement can play additional therapeutically protective roles besides the usually expected role for potential thrombotic occlusion:

Animal Models for Evaluating Endovascular Intervention

Among animal models for endovascular intervention evaluation, the canine venous pouch model and the rabbit elastase model are most frequently used. In the present study, these were abstracted as the straight-vessel (sidewall) model and the curved vessel model, respectively. The rabbit elastase model is anatomically closer to human cerebral aneurysms.^6,21 Consistent with the histology of human intracranial aneurysms, the elastase-created aneurysm wall has a disrupted or disappearing internal elastic lamina, a thinned tunica media, and some limited inflammatory cell deposition and thrombosis. The vessel diameter in the rabbit model approximates that of the middle cerebral artery in humans, and the blood pressure and coagulation system are similar as well. Conversely, the canine model is simpler to create and thus still widely used.^22,23 To our knowledge, no study has examined the hemodynamic implications of placing a stent on a curved-versus-straight vessel with a saccular aneurysm.

We have shown distinct flow mechanisms between the 2 types of aneurysm geometries, which lead to different flow modifications after stent placement. The canine model might give a false-positive indication of the stent inducing thrombotic occlusion. A model capturing the vessel geometry (on a curve, at a bifurcation, or both) of human cerebral aneurysms will give more reliable hemodynamic indication of endovascular intervention results. In this sense, our hemodynamic study further supports that the rabbit elastase model is a more realistic aneurysm model than the canine model.