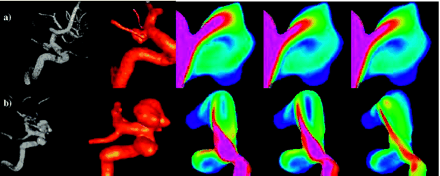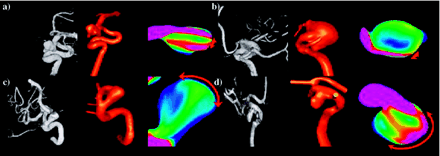Abstract
BACKGROUND AND PURPOSE: Hemodynamic factors are thought to play an important role in the initiation, growth, and rupture of cerebral aneurysms. This report describes a pilot clinical study of the association between intra-aneurysmal hemodynamic characteristics from computational fluid dynamic models and the rupture of cerebral aneurysms.
METHODS: A total of 62 patient-specific models of cerebral aneurysms were constructed from 3D angiography images. Computational fluid dynamics simulations were performed under pulsatile flow conditions measured on a normal subject. The aneurysms were classified into different categories, depending on the complexity and stability of the flow pattern, the location and size of the flow impingement region, and the size of the inflow jet. The 62 models consisted of 25 ruptured and 34 unruptured aneurysms and 3 cases with unknown histories of hemorrhage. The hemodynamic features were analyzed for associations with history of rupture.
RESULTS: A large variety of flow patterns was observed: 72% of ruptured aneurysms had complex or unstable flow patterns, 80% had small impingement regions, and 76% had small jet sizes. By contrast, unruptured aneurysms accounted for 73%, 82%, and 75% of aneurysms with simple stable flow patterns, large impingement regions, and large jet sizes, respectively. Aneurysms with small impingement sizes were 6.3 times more likely to have experienced rupture than those with large impingement sizes (P = .01).
CONCLUSIONS: Image-based patient-specific numeric models can be constructed in an efficient manner that allows clinical studies of intra-aneurysmal hemodynamics. A simple flow characterization system was proposed, and interesting trends in the association between hemodynamic features and aneurysmal rupture were found. Simple stable patterns, large impingement regions, and jet sizes were more commonly seen with unruptured aneurysms. By contrast, ruptured aneurysms were more likely to have disturbed flow patterns, small impingement regions, and narrow jets.
Cerebral aneurysms are pathologic dilations of the arterial wall that frequently occur near arterial bifurcations in the circle of Willis (1–3). The most serious consequence is their rupture and intracranial hemorrhage into the subarachnoid space, with an associated high mortality and morbidity rate (4–7). Greater availability and improvement of neuroradiologic techniques have resulted in more frequent detection of cerebral aneurysms before rupture. Because the prognosis for subarachnoid hemorrhages (SAHs) is still poor, aneurysmal obliteration is a necessary therapeutic option. Planned aneurysm surgery could benefit from a better understanding of the process of aneurysm formation, progression, and rupture so sound judgment in balancing the risks and benefits of possible therapies can be exercised.
The genesis, progression, and rupture of cerebral aneurysms are not well understood. The evolution of an aneurysm may be affected by variety of factors, including the material behavior of the vessel wall and the intra-aneurysmal hemodynamics. Intra-aneurysmal hemodynamic factors are thought to be important in both the pathogenesis and thrombosis of cerebral aneurysms (8); however, the relative importance of these factors and their interaction is not well understood.
The flow dynamics of cerebral aneurysms have been studied in numerous experimental models and clinical studies to investigate the role of hemodynamic forces in the initiation, growth, and rupture of cerebral aneurysms (9–16). Although this work has characterized the complexity of intra-aneurysmal hemodynamics in experimental and computational models, the studies have largely focused on idealized aneurysm geometry or surgically created aneurysms in animals. Each of these approaches has had significant limitations in connecting the hemodynamic factors studied to a clinical event. In vitro studies have allowed very detailed measurement of hemodynamic variables but are of limited value in understanding the hemodynamic forces in an individual clinical case because the creation of the patient-specific geometric models is currently impractical for large population studies. A correlation between patient-specific clinical events and hemodynamic patterns must be undertaken to better understand the relative importance of these forces.
Computation-based models provide an attractive method of making these correlations by providing the ability to theoretically model and study any possible geometries (17–20). Until recently, computational studies have been performed only on idealized aneurysm geometries or approximations of a specific patient geometry. The challenge in applying computational methods to large numbers of patient-specific aneurysm geometries can be divided into 3 major steps. The first step is obtaining the patient-specific geometry. The second is converting the geometry into a workable numeric model. The third step is performing the large numbers of calculations required for the clinical investigation.
With the development of CT angiography, MR angiography, and rotational cerebral angiography, patient-specific 3D geometries of cerebral aneurysms are readily available in modern cerebrovascular practices. Current imaging modalities are not adequate for in vivo quantification of intra-aneurysmal flow patterns. The geometric shape of aneurysms, however, can be accurately reconstructed from anatomic images. Rapid advances in computer science have reduced the cost of computational power. Consequently, the computational power required to perform the calculations necessary for large numbers of flow dynamic models has become more widely available. The obstacle for computational studies has been the difficulty in converting large numbers of patient-specific data into workable models for the hemodynamic study.
The purposes of our study were (1) to demonstrate the feasibility of using patient-specific 3D rotational angiography (3DRA) image data from clinical studies to construct corresponding realistic patient-specific computational fluid dynamics (CFD) models of cerebral aneurysms in a representative patient population, (2) to characterize these intra-aneurysmal flow patterns, and (3) to explore their possible associations with the clinical history of aneurysmal rupture.
Methods
Data and Image Acquisition
Between January 2003 and May 2004, 87 consecutive patients referred to the interventional neuroradiology service and diagnosed with one or more cerebral aneurysms by conventional catheter angiograms and 3DRA were identified. Cerebral angiograms were performed within 24 hours of presentation to the hospital for patients with a history of intracranial hemorrhage by interventional neuroradiologists (C.M.P., R.S.P.). All catheter angiograms were performed by standard transfemoral catheterizations of the cerebral vessels and digital subtraction imaging was performed with a Philips Integris biplanar unit (Philips Medical Systems, Best, The Netherlands). Rotational angiograms were performed by using a 6-second constant injection of contrast agent and a 180° rotation with imaging at 15 frames per second, for 8 seconds, for acquisition of 120 images. Data from these images were transferred to the Philips Integris workstation and reconstructed into 3D voxel data by using the standard proprietary software. 3D reconstructions were compared with views from the conventional angiogram to assess the completeness of the rendering. Aneurysms for which the 3DRAs did not contain the entire aneurysm or associated parent arteries were excluded from the analysis. The location of each aneurysm was recorded. Measurements of the aneurysm dome, neck, and associated parent artery were performed by using the conventional angiographic images and reference markers included in the view. The patient’s medical and radiologic records were reviewed and evaluated for evidence of aneurysmal intracranial hemorrhage. In patients with multiple aneurysms, clinical and radiologic information was considered and the most likely source of the hemorrhage was determined. The other coincident aneurysms were classified as unruptured. In cases where clinical information was inconclusive or not available, the aneurysms were classified as unknown. All measurements, classification of the aneurysms, and clinical evaluations were performed by interventional neuroradiologists (C.M.P., R.S.P.).
During the study period, 87 patients who were diagnosed with cerebral aneurysms by cerebral angiography and also had 3DRAs were considered for review. Of them, 30 were excluded from the study because 3DRA did not completely visualize all avenues of inflow to the aneurysm (eg, anterior communicating aneurysms with bilateral A1 contributions) or were technically inadequate. The patients ranged in age from 31 years to 88 years, with a mean age of 51 years; approximately two thirds of the patients were women and one third was men. Twenty-five had documented SAHs that could be attributed to an intracranial aneurysm. Nine patients had 2 aneurysms each, and one patient had 5. Two of these patients had a clinical history of SAH. For 3 patients, clinical information was incomplete or inconclusive, so whether 3 of the aneurysms were ruptured was unknown. These 3 aneurysms were excluded from the analysis. A total of 62 models of intracranial aneurysms in 57 patients were constructed from 3DRA images, including 25 ruptured aneurysms, 34 unruptured aneurysms, and 3 that were classified as unknown.
Computational Modeling
Vascular Modeling.
The voxel data were transferred from the Phillips Integris workstation to a PC computer for each of the selected cases. By using software developed by us, the data were processed to construct anatomic models for computational fluid dynamics calculations. In this process, the 3D visualization from the conventional angiogram was converted into a “watertight” (eg, with no holes, gaps, or intersecting or overlapping triangles) anatomic model of the aneurysm and connecting vessels while retaining the correct topology. This process avoids possible effects of thresholding and the associated possible distortion of the 3D model because the isosurface that is extracted is then deformed with a geometric deformable model that places the surface at the edges of the vessels by using calculated attenuation gradients between “pixels.” Therefore, the final result is independent of the threshold used to extract the first isosurface (21). The techniques involved in this process have been described elsewhere (22–24). The image processing, segmentation, surface reconstruction, and grid generation are a semiautomated process. The operator was blinded to the clinical history of prior aneurysmal rupture for all cases.
Flow Analysis.
The blood flow was modeled as an incompressible Newtonian fluid. The governing equations are the unsteady incompressible Navier-Stokes equations (25, 26). For simplicity and because of a lack of information regarding the distribution of vessel wall elasticity and thickness, the vessel walls were assumed to be rigid and no-slip boundary conditions were prescribed at the vessel walls. Non-Newtonian effects were neglected. Pulsatile velocity boundary conditions were imposed at the model inlet by using a superposition of Womersley velocity profiles for each Fourier mode of the prescribed flow rate curve (27, 28). Because no flow information was available for the patients included in this study, the flow rates were taken from phase-contrast MR measurements performed in the craniocervical arteries of a normal subject (29). These images were acquired on a 1.5T scanner (General Electric, Waukesha, WI) at an in-plane resolution of 0.58 mm, a section thickness of 3 mm, and a field of view of 15 cm. Only the velocity component normal to the section plane was imaged. These measurements were obtained for both internal carotid arteries, both middle cerebral arteries, both anterior cerebral arteries, and the basilar artery. Figure 1 shows the MRA of the normal subject (A), the vessels in the circle of Willis and the location of the PC-MR section planes (B), a sample section frame showing the magnitude (C) and the phase image (D), and the measured flow rate curve in the right internal carotid artery (E). The flow equations were numerically solved by using an implicit finite element formulation (30). One hundred time-steps per cardiac cycle were used, and the calculation was performed for 2 cardiac cycles. At each time-step, the discretized momentum equation was solved by using a generalized minimal residual solver while the pressure-Poisson equation was solved by using an incomplete lower-upper preconditioned conjugate gradient solver (31).
Physiologic flow conditions derived from PC-MR measurements on a normal subject. A, MRA. B, Vessels of the circle of Willis and location of PC-MR section planes. C, Magnitude image of PC-MR measurement. D, Phase image of PC-MR measurement. E, Flow rate curve obtained from the PC-MR measurement on the right internal carotid artery.
Postprocessing and Visualization
The entire time-dependent flow field computed by the finite element solver was stored at every time-step. This solution was then postprocessed to compute and visualize time-averaged wall shear stress (WSS), peak pressure, and oscillatory shear index (OSI). Animations were constructed to visualize the distribution of intravascular flow velocities across time as a cine loop containing superimposed 3D models at every time-step of the second cardiac cycle.
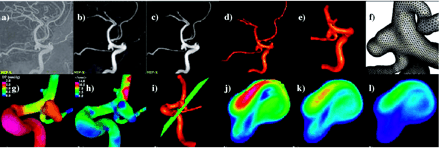
All the stages described above were performed by using a set of in-house software tools (32). This software has been extensively validated with in vivo patient-specific image data of carotid arteries (33, 34) and in vitro models of stenosed carotid (33) and renal arteries (35). The process of constructing a geometric model from the 3DRA images, which is the stage that requires most of the user interaction, takes a few hours, depending on the complexity of the aneurysm, the quality of the anatomic images, and on the level of expertise of the modeler. The generation of the finite element grid is then completely automatic and takes several minutes on a 3-GHz Pentium 4 with two gigabytes of random access memory. The CFD simulation comprising 2 cardiac cycles takes between 10 and 24 hours on the same computer, depending on the number of elements in the mesh. The complete process of model construction, meshing, CFD calculation, and visualization can be completed in a day. The vascular CFD modeling process is illustrated in Fig 2; the top row shows the original (unprocessed) 3DRA image (A), the image after smoothing with a combination of blurring and sharpening operators (B), the image after segmentation with a region growing algorithm (C), the initial anatomic model obtained by isosurface extraction (D), the final vessel geometry after deformable model and interactive truncation of arterial branches (E), and the surface of the tetrahedral finite element grid generated for the CFD calculation (F). The bottom row of Fig 2 shows examples of flow visualizations performed after solving the Navier-Stokes equations: surface pressure distribution (G), mean wall shear stress (H), location of a cut plane (I) used to visualize the time-dependent intra-aneurysmal velocity pattern (J–L).
Construction of a patient-specific vascular CFD model. A, Original 3DRA image. B, Smoothed image. C, Segmented image. D, Initial vascular reconstruction. E, Vessel geometry after deformable model and interactive truncation of arterial branches. F, Finite element grid. G, Peak pressure distribution. H, Mean wall shear stress distribution. I, Definition of cut plane used to visualize velocity pattern. J–L, Intra-aneurysmal flow velocity on cut plane at different instants during the cardiac cycle.
Data Analysis
Aneurysm Classification.
The anatomic and hemodynamic representations for each aneurysm were evaluated independently by 3 observers on a workstation (C.M.P., J.R.C., R.S.P.). Two of the observers had no special training in data processing but were asked to evaluate the images qualitatively on the basis of predetermined characteristics. The velocity pattern from the intra-aneurysmal flow velocity cine was classified in 4 ways: (1) complexity and stability of intra-aneurysmal flow by assigning one of 4 flow types, (2) the location of the apparent impingement (collision of the inflow jet with the wall of the aneurysm) as neck, body, dome, lobulation, or changing, (3) size of the zone of impingement compared with the size of the aneurysm as either large or small, and (4) size of the inflow jet compared with the largest dimension of the aneurysm and to the size of the aneurysm neck as large or small. Inflow jets or impingements were considered small if they were less than half the size of the reference dimension (ie, neck or dome diameter). The complexity and stability of flow were divided into 4 flow types: type I—unchanging direction of inflow jet with a single associated vortex; type II—unchanging direction of inflow jet with multiple associated vortices but no change in the number of vortices during the cardiac cycle; type III—changing direction of inflow jet with creation of a single vortex; and type IV—changing direction of the inflow jet with creation or destruction of multiple vortices. The observers were blinded to the clinical history of the patients. The categories were independently assigned by the observers and then compiled. In situations with intraobserver disagreements, all 3 observers reexamined the models to reach a consensus. The data were then analyzed to look for an association with the clinical history of aneurysm rupture.
Statistical Analysis.
Multiple logistic regression analysis was used to assess the effect of hemodynamic variables on risk of rupture while controlling for their effects on one another. Odds ratios (ORs) with 95% confidence interval (CIs) were calculated. The dependent variable for the model was rupture (yes/no), and most independent variables were also dichotomized: velocity (stable/other), jet size (small/large), and impingement size (small/large). Impinging location was trichotomized: neck/other, body/other, and dome/other. A P value <.05 was considered to be statistically significant. All analyses were carried out by using SAS software version 8.2 (SAS Institute, Cary, NC).
Results
Numeric Models
Data for the 62 aneurysms were used to construct visualizations for analysis. The morphology of the aneurysms was fairly evenly distributed between lateral (42%), bifurcation (27%), and terminal types (25%), with only a small minority of fusiform aneurysms (5%). The aneurysms ranged in size from 2 mm to 25 mm, with an average size of 8.4 mm. Separating them by largest dimension finds 31% small (≤5 mm), 56% medium (>5 mm and ≤15 mm), and 14% large (>15 mm). Aneurysms were fairly evenly distributed throughout the range of neck size indexes.
Hemodynamic Characterization
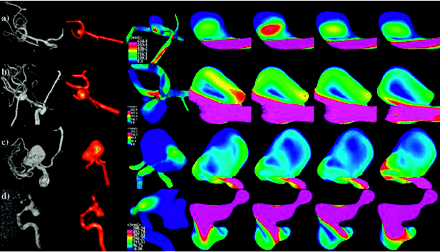
Intra-aneurysmal flow velocity visualizations show a great variety in flow patterns in the aneurysms studied. Each aneurysm has its own unique hemodynamic profile, but many aneurysms shared some characteristics. In all but one of the aneurysms, a single well-defined inflow jet could be discerned. In no aneurysm were multiple inflow jets present. The inflow jet most frequently entered the aneurysm neck on the distal portion of the neck and impacted the aneurysm wall, most frequently in the dome (47%), or body (27%) (Table 2). Only 20% of the aneurysms had flows impacting the aneurysm neck. In no aneurysm was the region of impingement within a secondary lobulation. Three aneurysms (5%) were classified as having a changing region of flow impingement, and all of them were ruptured. Figure 3 shows examples of aneurysms where the inflow jet impacts the aneurysm neck (A), body (B), or dome (C) or a changing impingement region (D). Although most frequently located on the distal portion of the neck, there were 4 aneurysms where the zone of inflow was actually into the proximal neck. Each of these aneurysms was associated with parent arteries with a significant curvature (eg, internal carotid siphon) that directed the flow into the proximal neck. After impinging on the wall of the aneurysm, the inflow jet dispersed into one or more vortices, depending on the geometry of the aneurysm. Figure 4 shows examples of an aneurysm with inflow jet located in the distal region of the neck (A) and another with the inflow jet in the proximal region of the neck (B). Outflow of the aneurysms was much more variable with some aneurysms with a single well-defined vortex forming a single outflow stream and others with less-well-defined flows. Flows into secondary lobulations were typically small slow-moving vortices and never accepted most inflow into the aneurysm.
Examples of aneurysms where the inflow jet impacts the neck (A), the body (B), or the dome (C) or has a changing impingement region (D). Images, from left to right, present volume rendering of 3DRA image, reconstructed model, mean wall shear stress distribution, and intra-aneurysmal flow velocity on a planar cut through the sac at 4 instants during the cardiac cycle.
Examples of aneurysms with inflow jet located in the distal (A) and proximal (B) region of the neck. Images, from left to right, present volume rendering of 3DRA image, reconstructed model, and intra-aneurysmal flow velocity on a planar cut through the sac at 3 instants during the cardiac cycle.
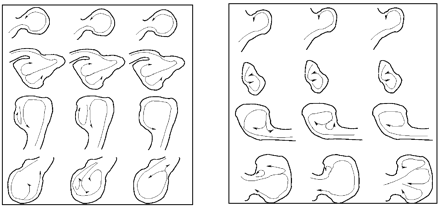
On the basis of our classification, type I flows (44%) were the most common, followed by type IV (20%), type II (19%), and type III (17%) (Table 1). All flow types were seen in the 2 most common locations—the posterior communicating internal carotid artery and middle cerebral artery (MCA). With the exception of 3 pericallosal ACA aneurysms, all locations had 2 or more different flow types represented in this series. In posterior communicating aneurysms, type IV (46%) was most common followed by type III (31%). For MCA aneurysms, type III (43%) and type I (29%) flow patterns were the most common. All the flow patterns were also seen in all the morphologic types except for fusiform aneurysms. Only type II and type IV were observed in this small subgroup. Type I flow patterns were the most frequent in lateral and bifurcation aneurysms. In terminal aneurysms, type I and III were seen with equal frequency—together representing 73% of the terminal aneurysms. All flow types were found in small aneurysms, but, as the aneurysm became larger, type II and type IV flow patterns predominated. Figure 5 shows a schematic drawing of the most prominent flow structure, illustrating the complexity and stability of the 4 flow types. The number of lobulations also did not predict flow type. Aneurysms with a single lobulation (one sac) most commonly had type I flows (59%), but all flow types were found in significant numbers. Multilobulated aneurysms (≥3 lobulations) had an even distribution of flow types II–IV, but no type I flows. The size of the zone of impingement, classified as either small or large relative to dome size, also appears to be independent of aneurysm size, size index, or the neck size index. Figure 6 shows examples of ruptured aneurysms with small flow impingement region (A and B) and unruptured aneurysms with large impingement regions (C and D).
Schematic drawings of the most prominent flow structures observed in small (left) and large (right) aneurysms with flow types I (top) through IV (bottom). Arrows indicate the direction of flow at 3 instants during the cardiac cycle and illustrate the complexity and stability of the intra-aneurysmal flow patterns for the 4 flow type categories.
Examples of small and large impact zones. A and B, Ruptured aneurysms with small flow impingement regions. C and D, Unruptured aneurysms with large impact zones. Red arrows indicate the flow impingement region.
Relationship between aneurysm flow pattern type and various anatomic characteristics
Hemodynamics and Rupture
The distribution of unruptured and ruptured aneurysms in the flow-related categories showed some interesting trends. In flow types I and II, unruptured aneurysms account for 73% and 55% of aneurysms in these groups, respectively (Table 2). In types III and IV, ruptured aneurysms exceed the number of unruptured aneurysms by small majorities, reaching 60% and 58% of the total, respectively. With regard to impingement zone location, ruptured aneurysms were found in every category (Table 2). Only in the dome category did the number of unruptured aneurysms exceed the number of ruptured aneurysms. All aneurysms with changing impingement regions were ruptured. The relative size of the impingement zone had a more striking difference (Table 2): 80% of ruptured aneurysms had small impingement zones, accounting for 65% of all aneurysms with small impingement zone; by contrast, unruptured aneurysms accounted for 82% of aneurysms with large impingement zones relative to the aneurysm dome size. Most ruptured aneurysms were found to have small jet sizes (76%), accounting for 54% of aneurysms in this category (Table 2). By contrast, 75% of aneurysms with large jet sizes were unruptured.
Relationship between rupture and location of the flow impingement region (IR), flow pattern (FP) type, size of the flow impingement region (IS), and size of the inflow jet (JS)
The associations between risk of rupture and specific hemodynamic characteristics are presented in Table 3. Of the 4 hemodynamic characteristics examined, only impingement size was associated with risk of rupture (OR = 6.3; 95% CI, 1.5–27; P = .01). Aneurysms with small impingement sizes were 6.3 times more likely to have experienced rupture than aneurysms with relatively large impingement zones.
Hemodynamic characteristics associated with rupture
Discussion
We have developed an efficient pipeline for constructing patient-specific computational models of cerebral aneurysms from medical 3D images. By using this pipeline, we were able to perform CFD analysis in a small series of patients with cerebral aneurysms from our clinical practice. All of these models were constructed to be patient-specific and as realistic as possible. From these models, we have developed a simple aneurysm characterization system based on the calculated hemodynamic features. This has enabled us to analyze the association of calculated patient-specific hemodynamic parameters with clinical information. Our study highlights the feasibility of using computational methods for clinical investigations as a bridge between laboratory studies of physiology and clinical outcomes. It also reveals the potential of using the CFD process to bring physiology to the day-to-day clinical practice of cerebrovascular disease.
In our series, simple stable patterns, large impingement regions, and large jet sizes were more commonly seen with unruptured aneurysms. By contrast, ruptured aneurysms were more likely to have disturbed flow patterns, small impingement regions, and narrow jets. Aneurysms with small impingement sizes were 6.3 times more likely to have experienced rupture compared with aneurysms with relatively large impingement zones (P = .01). Although not reaching statistical significance, intra-aneurysmal flow patterns with multiple vortices and/or unstable inflow jets (types II–IV), location of impingement region in the body or dome, and small jet size showed trends toward increasing the risk of prior rupture with P values of .08, .74, .97, and .45, respectively. These findings suggest that the characteristics of the inflow jet and its interaction with the aneurysm wall play an important role in the development and ultimate rupture of a cerebral aneurysm.
We found a great variety in patterns of intra-aneurysmal flow and hemodynamic stresses in our patient population. Each aneurysm has its own unique flow pattern, ranging from a simple single repetitive vortex to chaotic changing multiple vortices. All the aneurysms in this study have a single inflow jet, but the size of the jet, area involved in impingement with the aneurysm wall, and the angles of entry vary greatly. The wide variety of flow patterns led us to develop a simple classification of the aneurysm flow patterns based on the 2 major features common to all the aneurysms: the inflow jet and the number of vortices. The flow velocity cine visualizations in this study were divided by the complexity of secondary flows (vortices) and the stability of the direction of the inflow jet. As the most prominent flow feature, the inflow jet was used as the principal determinant. We reasoned that an unstable flow pattern could be associated with aneurysm progression and rupture because of the potential for elevated OSI or larger regions of elevated mean WSS. Alternatively, a stable pattern of repetitive forces may be more amenable to the arterial compensatory mechanisms for mitigating the stress, making these aneurysms safer.
Prior clinical studies of aneurysms have largely ignored the effects of the geometry of the parent artery, and its relationship to the aneurysm. Extremes in parent artery configuration can cause extensive changes in the flow within an aneurysm. For example, it can cause deflection of the inflow jet away from its typical location in the distal lip of the aneurysm, in effect converting a sidewall aneurysm to a flow pattern analogous to a terminal aneurysm with the inflow jet impacting the dome or entering the proximal neck. In our series, we found 4 aneurysms where this effect was clearly present (eg, Fig 4B). With recognition of this possibility, some of the effect of parent artery geometry can be intuitively predicated on inspection, but the complexity of rotatory flow patterns from the 3D nature of the geometry can lead to mistakes. On the basis of our analysis, we believe that CFD methods are necessary to produce accurate assessments of flow patterns.
The intra-aneurysmal flow is not easily predictable on the basis of simple morphology (number of lobulations, location, occurrence at vessel branching points) or aneurysmal measurements (aneurysm size, aspect ratio, or neck size). Intra-aneurysmal flow patterns on cine velocity visualizations varied greatly within the study group aneurysms. For example all flow types were found in the middle cerebral bifurcation and posterior communication aneurysms. This was also true for aneurysm morphologic types and aneurysms sizes. Certainly, for smaller aneurysms the simpler type I pattern was more common, but type IV and III flows were seen in significant numbers. Furthermore, components of the flow were not easily assigned on the basis simple inspection. Large neck size or large aneurysm size did not equate with large inflow jets or impingement regions.
There are several factors that account for this. As seen in our prior sensitivity analysis (24), small variations in the geometry of an aneurysm have significant effects on flow patterns due to the nonlinear character of the Navier-Stokes equations. Although many anatomic measures have been shown to have clinical associations with ruptured aneurysms, these relatively crude measures may not be sufficient to describe the complex geometry of aneurysms. For example, aneurysms of vastly dissimilar shape can have a common maximum dimension, neck, or even aneurysm volume. Intuitively, we would predict a similarly wide variation in flow patterns, stresses, and pressure consistent with the findings in our study. The classical descriptions of aneurysm morphology type (eg, lateral, terminal, bifurcation, or fusiform) or number of lobulations are only modest qualitative improvements. Multilobulated aneurysms appear to be a marker for more complex aneurysm flow patterns, but complicated flow types were also seen in aneurysms with a single lobulation. The incorporation of branching flows in bifurcation and terminal aneurysms or aneurysms involving collateral pathways (eg, aneurysms of the anterior communicating complex) add another layer of complexity.
Although the data from our study appear to suggest that hemodynamic characteristics determined by CFD analysis can be helpful in assessing the risk of cerebral aneurysm rupture, these data should be considered preliminary. Care must be taken in generalizing our findings to all cerebral aneurysms because of several limitations that may have prevented us from identifying other important associations. This study relies on an assumption that the aneurysm anatomy is little changed by the event of rupture; however, an aneurysm may undergo a variety of structural changes during and immediately after a hemorrhage. For example, a portion of the aneurysm may be filled with thrombus or a new daughter sac may form. As reported elsewhere in our sensitivity analysis (24), small changes in the geometry can have significant effects on intra-aneurysmal patterns. Therefore, it may be necessary to conduct prospective natural history studies of CFD-analyzed unruptured aneurysms to evaluate conclusively the association of a predetermined hemodynamic factor to risk of aneurysmal rupture.
The study population, though large for a CFD study, is small compared with the large variety of aneurysms seen in clinical practice. Therefore, only a few examples of each aneurysm location are represented in this study. Because of technical limitations, no aneurysms from the anterior communicating artery were included in this study. We attempted to include consecutive aneurysms seen in our practice prospectively, but many of the aneurysms that were diagnosed could not be included. The issues involved in this could introduce a bias in our sample.
Beyond the potential statistical problems found in all clinical studies, there are several limitations to the CFD process that could affect our results. Like all the previously reported CFD studies, we used a number of assumptions in modeling of intra-aneurysmal flow dynamics, which may lead to differences between the calculated flow patterns and the in vivo state. Unlike several earlier CFD studies, our models are constructed to duplicate the patient-specific anatomy and are performed under pulsatile flow conditions. We took great care in maintaining the geometric relationships of the adjacent parent artery and aneurysm sac, but this is impractical to extend to the entire circulation. Therefore, a model is studied in isolation from the surrounding vasculature of the cerebral circulation. This requires certain assumptions and approximations be made for the flow conditions. Small adjacent arteries are not modeled and flow rates through larger distal arteries are determined on the basis of geometry rather than distal physiologically determined resistances of the small arterioles and capillary beds. The input flows used for our models were not patient specific, but relied on measurements made from a normal volunteer. Frequency (pulse rates) was held constant and arbitrarily set at 60 beats per minute. With rigid walls and Newtonian flows, transmission of forces is theoretically instantaneous and therefore would not be expected to significantly affect the results of our simulations. Nevertheless, it has to be considered with the introduction of non-Newtonian flow and elastic vascular walls. Although the flow information may represent a reasonable estimate of conditions, ideally, patient-specific flow conditions should be known for each patient for the possible range of physiologic variations they might experience. Because these measurements are not normally obtained as a part of standard clinical practice, these data were not available for use for the current study. Patient-specific flow information could readily be used, however, if it became available. Finally, the CFD process used in this study also makes 2 assumptions for the numerical models that clearly differ from the in vivo cerebral aneurysm: Newtonian flow and rigid vessel walls. Most prior work by using CFD of aneurysms has used Newtonian fluid characteristics (ie, the fluid stress is proportional to the strain rate of the fluid), arguing that in large arteries with relatively high flow rates blood acts as a Newtonian fluid. In large aneurysms with slow areas of recirculation and zones of slow flow, the appropriateness of this assumption is unknown.
Overcoming the previously described limitations may not be possible until more information becomes available about aneurysms. For instance, a rigid wall model was chosen because of the limited availability of physical information of arterial wall properties such as elasticity and thickness. The intra-arterial pressure waveforms needed to prescribe physiologically correct boundary conditions for fluid-structure interaction algorithms are likewise unavailable. Pulsatile motion of the vessels is another effect that may be important for the accurate determination of intra-aneurysmal flow patterns. It is not currently possible to obtain reliable 4D images of the vasculature that would visualize the motion of the aneurysm and connected vessels. These features can be readily incorporated into the CFD calculations as information regarding these input variables becomes known. Thus, better and more reliable CFD modeling will become possible as techniques for intravascular physiologic measurements in cerebral arteries are developed.
The CFD process requires validation by using in vitro, animal, and in vivo data before making generalized statements about aneurysm hemodynamics. Determining the accuracy of the computational models will be critical before any quantitative study of hemodynamic forces. These flow-related forces have the potential to be the input function for further CFD models incorporating the mechanical properties of vessels walls for study of material failure rates. Preliminary validation studies of our CFD methodology in carotid arteries by using MR imaging and sonography flow data are ongoing with encouraging results (34), but further work needs to be done on aneurysmal vascular systems.
Even though there are some theoretical and practical limitations of the CFD visualizations we constructed for this study, analysis of these visualizations will be useful in refining our models in the future by allowing us to focus on hemodynamic and structural parameters common to clinically ruptured aneurysms. CFD provides an almost unlimited number of options for displaying information related to aneurysmal flow dynamics. Our scheme of analysis was intended to be simple but covering many of the parameters identified from prior research into aneurysmal hemodynamics. Our visualizations and analyses are intended as the starting point for more sophisticated and detailed evaluation of associations identified in this study.
Acknowledgments
We thank Richard Kemkers and Philips Medical Systems for technical support and encouragement to carry out this project.
References
- Received January 14, 2005.
- Accepted after revision March 2, 2005.
- Copyright © American Society of Neuroradiology
In this issue
Jump to section
Related Articles
Cited By...
- Radiomic profiling of high-risk aneurysms with blebs: an exploratory study
- Modeling Flow in an In Vitro Anatomical Cerebrovascular Model with Experimental Validation
- Insights into the pathogenesis of cerebral fusiform aneurysms: high-resolution MRI and computational analysis
- Associations between haemodynamics and wall enhancement of intracranial aneurysm
- Nature, content and shifts over time of the most impactful unruptured intracranial aneurysms articles: a bibliometric analysis
- Comparing Morphology and Hemodynamics of Stable-versus-Growing and Grown Intracranial Aneurysms
- Quantitative and Qualitative Comparison of 4D-DSA with 3D-DSA Using Computational Fluid Dynamics Simulations in Cerebral Aneurysms
- Quantification of hemodynamic irregularity using oscillatory velocity index in the associations with the rupture status of cerebral aneurysms
- Selective compromise of hypoplastic posterior communicating artery variants with aneurysms treatable by coil embolization: clinical and radiologic outcomes
- Towards the Clinical utility of CFD for assessment of intracranial aneurysm rupture - a systematic review and novel parameter-ranking tool
- Hemodynamic characteristics of stable and unstable vertebrobasilar dolichoectatic and fusiform aneurysms
- Identification of Hostile Hemodynamics and Geometries of Cerebral Aneurysms: A Case-Control Study
- Nonsphericity Index and Size Ratio Identify Morphologic Differences between Growing and Stable Aneurysms in a Longitudinal Study of 93 Cases
- Flow Diversion with Low-Profile Braided Stents for the Treatment of Very Small or Uncoilable Intracranial Aneurysms at or Distal to the Circle of Willis
- Computational fluid dynamics of cerebral aneurysm coiling using high-resolution and high-energy synchrotron X-ray microtomography: comparison with the homogeneous porous medium approach
- Hemodynamic differences between unstable and stable unruptured aneurysms independent of size and location: a pilot study
- Flow Conditions in the Intracranial Aneurysm Lumen Are Associated with Inflammation and Degenerative Changes of the Aneurysm Wall
- Assessment of intracranial aneurysm rupture based on morphology parameters and anatomical locations
- Evidence That a Subset of Aneurysms Less Than 7 mm Warrant Treatment
- Clinical, morphological, and hemodynamic independent characteristic factors for rupture of posterior communicating artery aneurysms
- Inflow Jet Patterns of Unruptured Cerebral Aneurysms Based on the Flow Velocity in the Parent Artery: Evaluation Using 4D Flow MRI
- Hemodynamics in growing and stable cerebral aneurysms
- Hemodynamic characteristics of large unruptured internal carotid artery aneurysms prior to rupture: a case control study
- Additional Value of Intra-Aneurysmal Hemodynamics in Discriminating Ruptured versus Unruptured Intracranial Aneurysms
- Morphologic and Hemodynamic Risk Factors in Ruptured Aneurysms Imaged before and after Rupture
- Morphologic and hemodynamic analysis of paraclinoid aneurysms: ruptured versus unruptured
- CFD: Computational Fluid Dynamics or Confounding Factor Dissemination? The Role of Hemodynamics in Intracranial Aneurysm Rupture Risk Assessment
- Generalized versus Patient-Specific Inflow Boundary Conditions in Computational Fluid Dynamics Simulations of Cerebral Aneurysmal Hemodynamics
- Rupture-Associated Changes of Cerebral Aneurysm Geometry: High-Resolution 3D Imaging before and after Rupture
- Computational fluid dynamics simulation of an anterior communicating artery ruptured during angiography
- Distinct trends of pulsatility found at the necks of ruptured and unruptured aneurysms
- Quantifying the Large-Scale Hemodynamics of Intracranial Aneurysms
- Role of Fluid Dynamics and Inflammation in Intracranial Aneurysm Formation
- Geometric, Hemodynamic, and Pathological Study of a Distal Internal Carotid Artery Aneurysm Model in Dogs
- 3D Cine Phase-Contrast MRI at 3T in Intracranial Aneurysms Compared with Patient-Specific Computational Fluid Dynamics
- 3D Computational Fluid Dynamics of a Treated Vertebrobasilar Giant Aneurysm: A Multistage Analysis
- Computational fluid dynamics simulation of an anterior communicating artery ruptured during angiography
- Thrombosis Heralding Aneurysmal Rupture: An Exploration of Potential Mechanisms in a Novel Giant Swine Aneurysm Model
- Intracranial Aneurysm Neck Size Overestimation with 3D Rotational Angiography: The Impact on Intra-Aneurysmal Hemodynamics Simulated with Computational Fluid Dynamics
- Comparison of Phase-Contrast MR Imaging and Endovascular Sonography for Intracranial Blood Flow Velocity Measurements
- Newtonian viscosity model could overestimate wall shear stress in intracranial aneurysm domes and underestimate rupture risk
- Effects of Perianeurysmal Environment during the Growth of Cerebral Aneurysms: A Case Study
- Hemodynamic Differences Between Unruptured and Ruptured Intracranial Aneurysms During Observation
- 1-Hexyl n-cyanoacrylate compound (Neucrylate™ AN), a new treatment for berry aneurysm. III: Initial clinical results
- Risk Analysis of Unruptured Aneurysms Using Computational Fluid Dynamics Technology: Preliminary Results
- Influence of Hemodynamic Factors on Rupture of Intracranial Aneurysms: Patient-Specific 3D Mirror Aneurysms Model Computational Fluid Dynamics Simulation
- High Shear Stress and Flow Velocity in Partially Occluded Aneurysms Prone to Recanalization
- Hemodynamics of Cerebral Aneurysm Initiation: The Role of Wall Shear Stress and Spatial Wall Shear Stress Gradient
- Patient-Specific Computational Hemodynamics of Intracranial Aneurysms from 3D Rotational Angiography and CT Angiography: An In Vivo Reproducibility Study
- Hemodynamics and Anatomy of Elastase-Induced Rabbit Aneurysm Models: Similarity to Human Cerebral Aneurysms?
- Association of Hemodynamic Characteristics and Cerebral Aneurysm Rupture
- MR Imaging of Partially Thrombosed Cerebral Aneurysms: Characteristics and Evolution
- Quantitative Characterization of the Hemodynamic Environment in Ruptured and Unruptured Brain Aneurysms
- Hemodynamic-Morphologic Discriminants for Intracranial Aneurysm Rupture
- In Vitro Study of Near-Wall Flow in a Cerebral Aneurysm Model with and without Coils
- Aneurysm Inflow-Angle as a Discriminant for Rupture in Sidewall Cerebral Aneurysms: Morphometric and Computational Fluid Dynamic Analysis
- Treatment of Intracranial Aneurysms by Functional Reconstruction of the Parent Artery: The Budapest Experience with the Pipeline Embolization Device
- Blood-Flow Characteristics in a Terminal Basilar Tip Aneurysm Prior to Its Fatal Rupture
- Intracranial Blood-Flow Velocity and Pressure Measurements Using an Intra-Arterial Dual-Sensor Guidewire
- Hemodynamics and Bleb Formation in Intracranial Aneurysms
- Quantitative Hemodynamic Analysis of Brain Aneurysms at Different Locations
- The Asymmetric Vascular Stent: Efficacy in a Rabbit Aneurysm Model
- Hemodynamic Patterns of Anterior Communicating Artery Aneurysms: A Possible Association with Rupture
- Hemodynamics in a Lethal Basilar Artery Aneurysm Just before Its Rupture
- Determination of Wall Tension in Cerebral Artery Aneurysms by Numerical Simulation
- Asymmetric Vascular Stent: Feasibility Study of a New Low-Porosity Patch-Containing Stent