Abstract
BACKGROUND AND PURPOSE: Compared with conventional T2-weighted MR imaging, diffusion tensor MR imaging provides quantitative indices with increased specificity to the most destructive aspects of multiple sclerosis. In this study, we obtained brain mean diffusivity (D̄) and fractional anisotropy histograms of patients with multiple sclerosis to compare them with those of healthy volunteers and to investigate the correlation between diffusion tensor MR imaging histogram-derived measures and the level of disability and quantities derived from conventional MR imaging.
METHODS: Dual-echo and diffusion tensor MR images were obtained from 78 patients with relapsing-remitting, secondary progressive, or primary progressive multiple sclerosis and from 20 healthy control volunteers. After obtaining mean diffusivity (D̄) and fractional anisotropy images and image coregistration, D̄ and fractional anisotropy histograms were created. From each histogram, the following measures were derived: the average D̄ and fractional anisotropy, the histogram peak heights, and the histogram peak locations.
RESULTS: All the D̄ and fractional anisotropy histogram-derived measures were different between patients and controls at a significance level of P < .001. No differences were found in any of the considered quantities among the three multiple sclerosis phenotypes. In patients with relapsing-remitting multiple sclerosis, disability was correlated with histogram average D̄ (r = 0.4, P = .01) and peak height (r = −0.4, P = .01). In patients with secondary progressive multiple sclerosis, disability was correlated with fractional anisotropy histogram peak position (r = −0.6, P = .01). Significant correlations were also found between T2 lesion load and various diffusion tensor MR quantities.
CONCLUSION: This study shows that brain D̄ and fractional anisotropy histograms are different for patients with multiple sclerosis compared with control volunteers. This study also shows that quantities derived from diffusion tensor MR imaging are correlated with disability in patients with relapsing-remitting multiple sclerosis and secondary progressive multiple sclerosis, suggesting that they might serve as additional measures of outcome when monitoring multiple sclerosis evolution in these patients.
Quantitative MR techniques are becoming increasingly important in the assessment of multiple sclerosis (1, 2). This is because they provide objective information that is complementary to and partially independent of that of conventional MR imaging. Conventional MR imaging lacks specificity to the heterogeneous aspects of multiple sclerosis (1, 2) and is unable to detect subtle changes occurring in the normal-appearing white matter (3–5). Diffusion-weighted MR imaging is one of the most promising techniques to go some way toward such limitations.
Diffusion-weighted MR imaging measures the microscopic random translational motion of water molecules (6). This motion is the result of the interactions with other molecules and with barriers that can “restrict” it (7). Barriers restricting water molecular motion are of particular interest in biological tissues, in which diffusion abnormalities can reflect changes of the tissue organization at a microscopic level (8). In highly organized systems, such as the brain white matter, the hindrance of water is not the same in all directions, as a consequence of structural geometry. This property is termed anisotropy and results in a variation of the measured diffusion coefficient with measurement direction (9–11). Therefore, in a 3D view, diffusion cannot be described by a scalar coefficient, and a mathematical entity, called the diffusion tensor, is needed to fully characterize the motion of water molecules (12). From diffusion tensor MR imaging, it is possible to derive some scalar indices, invariant to the changes in the frame of reference, which reflect the diffusion characteristics (and, hence, the integrity and organization) of the tissue. These measures include the mean diffusivity (D̄) (equal to one third of the trace of the diffusion tensor), which is a measure of the average molecular motion independent of any tissue directionality and is affected by cellular size and integrity (12, 13), and the fractional anisotropy, which is one of the most used measures of deviation from isotropy (14) and reflects the degree of alignment of cellular structures within fiber tracts, as well as their structural integrity.
In cases of multiple sclerosis, diffusion-weighted and diffusion tensor MR imaging can provide information that is inaccessible with other MR imaging techniques about structural changes caused by the two major pathologic aspects of the disease: inflammation and neurodegeneration (15–17). Previous reports (15–22) found that T2-visible multiple sclerosis lesions have water diffusivity that is higher and fractional anisotropy that is lower than the corresponding quantities of the normal-appearing white matter, which are, in turn, different from those of white matter from healthy volunteers. The majority of previous studies assessed D̄ and fractional anisotropy changes by using region of interest analysis (15–20). Region of interest analysis, however, is time-consuming, operator-dependent, prone to partial volume artifacts, and unable to provide an overall assessment of tissue damage. Only two preliminary diffusion-weighted MR imaging studies assessed D̄ changes in multiple sclerosis globally, by using histogram analysis (21, 22). These studies achieved encouraging results by showing marked differences of the D̄ histograms between control volunteers and patients (21, 22) and between patients with relapsing-remitting multiple sclerosis and those with and secondary progressive multiple sclerosis (22). However, they were not without limitations (including the size of the samples studied and the lack of histogram analysis of the fractional anisotropy distribution). As a consequence, their results need to be confirmed by a more complete analysis of a larger cohort of patients.
In this study, we assessed, using histogram analysis, the distributions of D̄ and fractional anisotropy in the brain tissue from a large group of patients with multiple sclerosis and compared them with those in the brain from healthy volunteers. We also investigated the magnitude of the correlation between diffusion tensor MR histogram-derived measures and the level of disability and the quantities derived from conventional MR imaging.
Methods
Patients
We studied 78 patients with multiple sclerosis (44 women and 34 men). None of these patients was included in our previous diffusion-weighted MR imaging studies of multiple sclerosis (17, 21). Their mean age was 43.6 years (SD = 10.6 years), the median duration of the disease was 10 years (range, 1–28 years), and the median Expanded Disability Status Scale (EDSS) score (23) was 5.0 (range, 0.0–8.5). According to the criteria presented by Lublin and Reingold (24), 28 of the patients were classified as having relapsing-remitting multiple sclerosis, 30 as having primary progressive multiple sclerosis, and 20 as having secondary progressive multiple sclerosis (Table 1). When MR images were obtained, none of the patients with relapsing-remitting multiple sclerosis and secondary progressive multiple sclerosis was experiencing an acute relapse or was being treated with corticosteroids. Twenty sex- and age-matched volunteers (12 women and eight men; mean age, 37.2 years; SD = 9.2 years) with no history of neurologic disorders and normal results of their neurologic examinations served as controls. Local Ethical Committee approval and written informed consent from all the volunteers were obtained before study initiation.
Demographic, clinical and conventional MR imaging characteristics of patients with three different MS clinical phenotypes
Image Acquisition
The following sequences were obtained from all the volunteers during a single imaging session by using a 1.5-T imager: dual-echo turbo spin-echo; 3300/16–98/1 (TR/TE/excitations); echo train length, 5; and pulsed-gradient spin-echo single shot echo-planar pulse sequence (inter-echo spacing = 0.8, TE = 123), with diffusion gradients applied in eight noncollinear directions, chosen to cover 3D space uniformly (25). The duration and maximum amplitude of the diffusion gradients were 25 ms and 21 mTm−1, respectively, giving a maximum b factor in each direction of 1044 s mm−2. To optimize the measurement of diffusion, only two b factors were used (26) (b1 ≈ 0, b2 = 1044 s mm−2). Fat saturation was performed using a four RF binomial pulse train to avoid chemical shift artifact. A birdcage head coil of ∼300 mm diameter was used for signal transmission and reception.
For the dual-echo images, 24 contiguous axial sections were acquired with 5-mm section thickness, 256 × 256 matrix, and 250 × 250 mm field of view. The sections were positioned to run parallel to a line that joins the most inferoanterior and inferoposterior parts of the corpus callosum (27). For the diffusion-weighted images, 10 axial sections with 5-mm section thickness, 128 × 128 matrix, and 250 × 250 mm field of view were acquired, with the same orientation of the dual-echo images, positioning the penultimate caudal section to match exactly the central sections of the dual echo. This brain portion was chosen because the periventricular area is a common location for multiple sclerosis lesions. In addition, these central sections are less affected by the distortions due to B0 field inhomogeneity, which can affect image coregistration.
Image Analysis and Postprocessing
All image postprocessing was performed on a workstation independent of the imager. After lesion identification by an experienced observer, hyperintense T2 volumes were measured by a trained technician using a semi-automated segmentation technique based on local thresholding (28). Additional details regarding lesion identification (28, 29) and lesion volume measurements (28) are provided elsewhere.
Diffusion-weighted images were first corrected for distortion induced by eddy currents using an algorithm that minimizes mutual information between the diffusion un-weighted and weighted images (30). Then, assuming a mono-exponential relationship between signal intensity and the product of the b matrix (a 3 × 3 matrix that expresses the relationship between the signal attenuation and the elements of the diffusion tensor matrix) and diffusion tensor matrix components, the diffusion tensor was calculated for each pixel according to the following equation: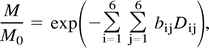 
where M is the measured signal intensity, M0 is the T2-weighted signal intensity, bij are the elements of the b matrix and Dij are the elements of the diffusion tensor matrix. The tensor was estimated statistically, using a nonlinear fitting of the data, according to the Marquardt-Levenberg method. After diagonalization of the matrix, D̄ and fractional anisotropy were derived for every pixel. The diffusion maps were interpolated to the same matrix size as the dual echo, and then the b = 0 step of the diffusion-weighted images (T2-weighted but diffusion unweighted) was coregistered with the T2-weighted images by using a surface-matching technique based on mutual information (30). The same transformation parameters and coregistration technique were then used to coregister D̄ and fractional anisotropy maps. Pixels containing CSF and extra-cerebral tissue were removed from the coregistered b = 0 step of the diffusion-weighted images, by using a semi-automated technique based on local thresholding (28). Next, the corresponding pixels were removed from fractional anisotropy and D̄ maps. Histograms were created from these maps by using 10% of the maximum wide bins. To compensate for differences in brain size, each bin was normalized by the total number of voxels contributing to the histogram. From each histogram, the following measures were derived: the average D̄ and fractional anisotropy, the histogram peak heights, and the histogram peak locations.
Because CSF removal from D̄ and fractional anisotropy maps is the only step of histogram creations that requires human intervention, this is the part of the procedure that can influence the reproducibility of the measurements. As a consequence, to verify the intra-rater reproducibility of the procedure, the same observer, unaware of to whom the images belonged, repeated twice the outlining of the brain from 10 randomly selected patients. The mean intra-rater coefficient of variation of the number of selected brain voxels included in histogram analysis was 1.5% (range = 0.2–2.7%).
Statistical Analysis
A Student t test for non-paired data was used to compare D̄ and fractional anisotropy histogram-derived measures between patients with multiple sclerosis and healthy control volunteers and among the three different multiple sclerosis phenotypes. We used Bonferroni correction to take into account these multiple comparisons. As a consequence, only P values ≤ .01 were considered significant. Correlations were assessed by using the Spearman Rank Correlation Coefficient.
Results
No abnormalities were seen on any of the conventional MR images obtained from the control volunteers. In the overall multiple sclerosis population, the median T2 lesion volume was 18.7 mL (range, 0.4–106.9 mL). In Table 1, T2 lesion volumes are reported separately for each of the clinical phenotypes.
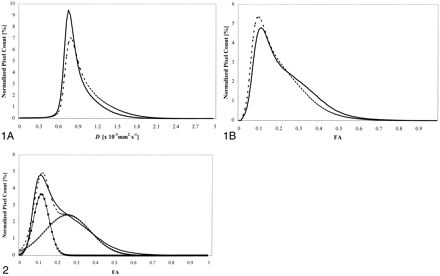
D̄ and fractional anisotropy histograms of patients and control volunteers are reported in Figure 1. Table 2 reports the mean value and SD of D̄ and fractional anisotropy from the overall patient population and control volunteers. All the considered quantities were different between the two groups at a significance level of P < .001. No differences were found in any of the considered quantities among the three multiple sclerosis phenotypes (data not shown).
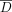and FA histogram-derived measures from MS patients and control subjects
Average histograms from patients with multiple sclerosis (dashed line) and control volunteers (continuous line).
A, Mean diffusivity (D̄).
B, Fractional anisotropy (FA).
fig 2. Average histogram of fractional anisotropy (FA) from control volunteers (thick continuous line). This curve can be fitted by the superimposition of two theoretical gaussian curves, representing the distribution of fractional anisotropy values of gray (filled squares) and white (open triangles) matter. Height, mean, and SD of these curves can be estimated by minimizing the difference between the sum (dotted line) and the actual histogram. See the text for further details
In the overall patient population and in patients with primary progressive multiple sclerosis, there was no significant correlation between histogram measures and clinical disability. However, when considering in isolation those patients with relapsing-remitting multiple sclerosis, the EDSS score was moderately correlated with histogram average D̄ (r = 0.4, P = .01) and peak height (r = −0.4, P = .01). When considering in isolation those patients with secondary progressive multiple sclerosis, the EDSS score was correlated with fractional anisotropy histogram peak position (r = −0.6, P = .01). Significant correlations were found between T2 lesion load and each of the following: histogram average D̄ (r = 0.4, P = .002), peak height (r = −0.3, P = .008) and peak position (r = 0.4, P = .001), and histogram average fractional anisotropy (r = −0.6, P < .001) and peak height (r = 0.3, P = .006). In patients, average D̄ was correlated with average fractional anisotropy (r = −0.4, P < .001). Such correlation was still present when considering each multiple sclerosis phenotype in isolation (data not shown), as well as when considering control volunteers (r = −0.7, P = .002).
Discussion
In this study, we obtained D̄ and fractional anisotropy histograms of a large portion of the brain from 78 patients with multiple sclerosis and 20 healthy volunteers. For D̄ histograms, we confirmed and extended the results of two preliminary studies (21, 22) by showing that patients with multiple sclerosis, independently of clinical phenotype, show a higher average D̄ and D̄ histogram peak position and a lower D̄ histogram peak height than do healthy volunteers. Clearly, these results are affected by the presence of multiple sclerosis lesions, and the impact of the contribution of lesions to the histograms can be seen by the correlation we found between T2 lesion volume and average D̄. However, because we analyzed large brain volumes, normal-appearing white matter is also likely to play a part in the histogram abnormalities. Histogram broadening and the consequent decrease of peak height shows that fewer pixels in the brain have normal D̄ values. The peak height is therefore an index of the remaining healthy tissue, which can be helpful in quantifying the more diffuse aspects of the disease.
In this study, we also analyzed, for the first time, the characteristics of fractional anisotropy histograms of healthy control volunteers and patients with multiple sclerosis and found that patients with multiple sclerosis have significantly lower histogram average fractional anisotropy and peak location and significantly higher peak height. As readily apparent from Figure 1, image intensity of fractional anisotropy maps has a different distribution than that of D̄ maps. D̄ histograms are bell-shaped curves, which can be interpreted as values distributed around a central bin, which represents the most common and “normal” value of the distribution. As a consequence, we interpret histogram broadening and the consequent decrease of the peak height to be the result of fewer pixels with normal D̄ values. The same does not apply to fractional anisotropy histograms. This is because gray matter and white matter have very different fractional anisotropy distributions. Although the D̄ values of these two tissues are very similar (at least for b factors of approximately 1000 smm−2), gray matter and white matter are characterized by different anisotropy behavior (13). Gray matter has a randomly ordered microstructure (at least on a voxel scale) and, therefore, it is almost isotropic to water diffusion. On the contrary, white matter is extremely anisotropic because it is constituted by highly oriented structures, such as myelin sheaths and axons. Thus, because fractional anisotropy histograms are created from images containing both gray matter and white matter, they are necessarily the result of the superimposition of two different bell-shaped curves.
Figure 2 shows that the average fractional anisotropy histogram of our control group can be fitted accurately by the sum of two gaussian curves, representing the theoretical distribution of fractional anisotropy in the gray and white matter in isolation. The parameters that characterize these two gaussian curves (amplitude, mean and SD) were estimated by progressively minimizing the difference between their sum (Fig 2, dotted line) and the actual fractional anisotropy histogram. The initial values of the parameters of the theoretical distributions of fractional anisotropy values in gray and white matter were obtained by averaging values measured using square regions of interest located by experienced observers in different white and gray matter structures of the brain from healthy control volunteers (31). The analysis of the distribution of fractional anisotropy values, as shown in Figure 2, helps in understanding the meaning of the fractional anisotropy histogram changes observed in patients with multiple sclerosis when compared with controls. The theoretical gaussian curve of white matter is much wider than that of gray matter. This is the consequence of the known intra-individual variations of fractional anisotropy values in different regions of the brain, due to the highly variable degree of coherence of fiber tract directions. Fractional anisotropy values are high in some structures, such as the corpus callosum or the internal capsules, where fibers have a parallel orientation, whereas fractional anisotropy values are relatively low in white matter regions, such as in the centra semiovale, where different tissue orientations are present within the same voxel. As a consequence, observed fractional anisotropy histogram peak location from control volunteers is close to the theoretical peak location of gray matter fractional anisotropy histogram. In case of brain pathologic abnormality with the potential to reduce white matter fiber tract organization, a shift of white matter fractional anisotropy histogram toward lower values would result in an increase of the histogram peak height. As expected, a previous study (16) showed that lesions and normal-appearing white matter from patients with multiple sclerosis have significantly decreased fractional anisotropy when compared with normal white matter from control volunteers. Therefore, our results (lower histogram average fractional anisotropy and peak position and higher histogram peak height in patients with multiple sclerosis when compared with healthy control volunteers) indicate a global decrease in white matter fractional anisotropy due to both the presence of macroscopic multiple sclerosis lesions (which are likely to be the major contributor to the increase of the histogram peak height) and diffuse normal-appearing white matter pathologic abnormality (which is likely to contribute to the shift toward the left of the histogram peak position).
In this study, we have also investigated whether differences in D̄ and fractional anisotropy histogram-derived measures were detectable among the three main different multiple sclerosis phenotypes. Contrary to what was found by a preliminary study comparing D̄ histograms from nine patients with relapsing-remitting multiple sclerosis and four with secondary progressive multiple sclerosis (22), we did not find any difference in D̄ and fractional anisotropy distributions among patients with relapsing-remitting multiple sclerosis, secondary progressive multiple sclerosis, and primary progressive multiple sclerosis. These results indicate that the overall severity of multiple sclerosis pathology is similar in these multiple sclerosis phenotypes. Considering that the loads of T2-visible lesions tend to be lower for patients with primary progressive multiple sclerosis than for those with secondary progressive multiple sclerosis (32), as also shown by the present study, this observation suggests that the relative contributions of the various aspects of the multiple sclerosis pathology to the accumulation of disability may vary in the two progressive forms of the disease. This agrees with the results of previous studies using magnetization transfer ratio histogram analysis (5, 33).
This study confirmed the presence of a significant correlation between D̄ and fractional anisotropy in association with multiple sclerosis (16). Nevertheless, the magnitude of the correlation that we found was far from being a strict relationship and was weaker than that found in control volunteers. This indicates that D̄ and fractional anisotropy provide complementary and partially independent information regarding multiple sclerosis pathology. Because tissue damage alone would both increase D̄ and decrease fractional anisotropy, this observation suggests the potential of serial diffusion tensor MR imaging to monitor tissue repair. For example, marked glial proliferation would decrease both D̄ and fractional anisotropy in concert, thus reducing the magnitude of the correlation that would result from a marked preponderance of tissue damage over tissue repair.
For patients with relapsing-remitting multiple sclerosis, measures derived from D̄ histograms were found to be significantly correlated, albeit moderately, with clinical disability, whereas EDSS scores were strongly correlated with fractional anisotropy peak positions for patients with secondary progressive multiple sclerosis. These correlations were not reported previously because of the small numbers of patients studied (15–22). These findings suggest that mechanisms leading to disability are likely to be different in patients with relapsing-remitting multiple sclerosis and secondary progressive multiple sclerosis. Although caution must be exercised, because this is a cross-sectional study, one might speculate that progressive loss of structural barriers to water molecular motion is a relevant pathologic aspect in relapsing-remitting multiple sclerosis, whereas loss of tissue organization, due to severe and repeated tissue damage, is one of the pathologic hallmarks of secondary progressive multiple sclerosis. Nevertheless, the magnitude of the correlation between diffusion tensor histogram-derived measures and disability was still perhaps disappointing. Several factors might explain this, including the many limitations of the EDSS score (34) and the role of spinal cord damage in determining neurologic disability (35).
Admittedly, the present study is not without limitations. The first is the relatively poor spatial resolution of the diffusion tensor MR images we used. Although our image resolution was similar to that of the two previous preliminary studies (21, 22), this may have led to partial volume effect in pixels located at the brain-CSF edge. However, these pixels are a small minority of the overall number of pixels contributing to the histograms and, as a consequence, partial volume effect can only partially explain the differences we found between patients and controls in D̄ and fractional anisotropy histograms. The use of pulse sequences with increased spatial resolution, such as interleaved echo-planar imaging sequences (36), should clarify this issue. The second limitation applies to all studies using histogram analysis of MR data. With such an approach, information related to the status of specific brain structures or tissues is inevitably lost. However, in the context of clinical trials, it may be unfeasible to measure D̄ or fractional anisotropy changes from several different brain regions and tissues, whereas a quantitative measure reflecting overall lesion burden might be a desirable outcome measure. In addition, because MR data are retrievable, D̄ and fractional anisotropy changes in specific areas or regions can always be measured, if needed.
Conclusion
This study shows that D̄ and fractional anisotropy histograms of a large portion of the brain are different in patients with multiple sclerosis compared with age- and sex-matched controls. These differences are likely to be the result of multiple sclerosis lesions and subtle changes in the normal-appearing white matter and suggest a net loss and disorganization of barriers restricting water molecular motion in the brain of patients with multiple sclerosis. This study also showed that D̄ and fractional anisotropy histogram-derived measures do not differ significantly among the three major clinical phenotypes of the disease but that some of them are correlated with the level of disability in patients with relapsing-remitting multiple sclerosis and secondary progressive multiple sclerosis. This suggests D̄ and fractional anisotropy histogram-derived measures as potentially useful measures of outcome to be used in addition to T2-weighted MR imaging when monitoring the evolution of relapsing-remitting multiple sclerosis and secondary progressive multiple sclerosis.
Footnotes
↵1 This study was generously supported by a grant from Federazione Italiana Sclerosi Multipla.
2 Address reprint requests to Massimo Filippi, MD, Neuroimaging Research Unit, Department of Neuroscience, Scientific Institute Ospedale San Raffaele, Via Olgettina, 60, 20132 Milan, Italy.
References
- Received August 7, 2000.
- Copyright © American Society of Neuroradiology
In this issue
Jump to section
Related Articles
Cited By...
- Patient-specific multi-modal modeling uncovers neurotransmitter receptor involvement in motor and non-motor axes of Parkinsons disease
- Simultaneous Super-Resolution and Distortion Correction for Single-shot EPI DWI using Deep Learning
- Rapid Microscopic Fractional Anisotropy Imaging via an Optimized Kurtosis Formulation
- Maturation of Brain Microstructure and Metabolism Associates with Increased Capacity for Self-Regulation during the Transition from Childhood to Adolescence
- Association of polygenic risk for major psychiatric illness with subcortical volumes and white matter integrity in UK Biobank
- Diffusion Tensor Analysis of Pediatric Multiple Sclerosis and Clinically Isolated Syndromes
- Brain Volume and Diffusion Markers as Predictors of Disability and Short-Term Disease Evolution in Multiple Sclerosis
- Multicentre imaging measurements for oncology and in the brain
- A diffusion tensor MRI study of patients with MCI and AD with a 2-year clinical follow-up
- Can imaging techniques measure neuroprotection and remyelination in multiple sclerosis?
- Influence of aging on brain gray and white matter changes assessed by conventional, MT, and DT MRI
- Enhanced visualization and quantification of magnetic resonance diffusion tensor imaging using the p:q tensor decomposition
- Diffusion Magnetic Resonance Histograms as a Surrogate Marker and Predictor of Disease Progression in CADASIL: A Two-Year Follow-Up Study
- Diffusion MRI in multiple sclerosis
- Mechanisms of normal appearing corpus callosum injury related to pericallosal T1 lesions in multiple sclerosis using directional diffusion tensor and 1H MRS imaging
- A review of structural magnetic resonance neuroimaging
- A diffusion tensor magnetic resonance imaging study of brain tissue from patients with migraine
- Coefficient Dav Is More Sensitive Than Fractional Anisotropy in Monitoring Progression of Irreversible Tissue Damage in Focal Nonactive Multiple Sclerosis Lesions
- Inter-Sequence and Inter-Imaging Unit Variability of Diffusion Tensor MR Imaging Histogram-Derived Metrics of the Brain in Healthy Volunteers
- Evidence for Cortical Functional Changes in Patients With Migraine and White Matter Abnormalities on Conventional and Diffusion Tensor Magnetic Resonance Imaging
- MRI techniques to monitor MS evolution: The present and the future