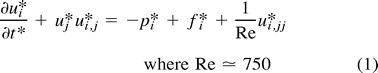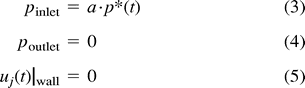Abstract
BACKGROUND AND PURPOSE: Distinguishing whether forces resulting from the impingement of central blood flow streams at a curved arterial segment or at the apex of an intracranial bifurcation could be important for the understanding of aneurysm formation. Using finite element models, our purpose was to investigate the hemodynamics related to intracranial saccular aneurysm formation through computer simulations.
METHODS: We present two-dimensional finite element models describing several distinct stages of aneurysm formation in both curved and bifurcating arteries. For each model, a description of the numeric solutions and results are presented.
RESULTS: Our results suggest that the pressures and shear stresses that develop along the outer (lateral) wall of a curved artery and at the apex of an arterial bifurcation create a hemodynamic state that promotes saccular aneurysm formation. The impingement of the central stream results in greatly increased velocity/pressure gradients and high shear stresses at the apex compared with those in the proximal parent or distal daughter branches. The results also indicate that the maximal pressure generated at the apex of the arterial bifurcation ranges from two to three times the peak luminal pressure in the proximal parent artery.
CONCLUSION: These data suggest that, in the absence of any underlying disease process, aneurysm development is a mechanically mediated event. These models offer a plausible hypothesis regarding the initiation, growth, and subsequent rupture of saccular intracranial aneurysms as they relate to the hemodynamics of intracranial arterial blood flow.
Hemodynamically generated forces resulting from the impingement of central blood flow streams either at a curved arterial segment or at the apex of an intracranial bifurcation could be an important contributing factor in the focal degeneration of the internal elastic membrane of the artery leading to aneurysm formation (1, 2). Essentially, there are three hemodynamic forces to consider: shear stress, impulse, and pressure. The computational model we use in this article previously has shown that the impingement of central flow streams results in greatly increased velocity/pressure gradients and high shear stresses at an arterial apex compared to those in the proximal parent or distal daughter branches. In addition, it has been demonstrated that the maximal pressure generated at the apex of the arterial bifurcation ranges from two to three times greater than the peak luminal pressure in the proximal parent artery (3).
These results may be explained by the observation that the momentum (momentum = mv, where m is the mass and v is the velocity) per unit volume of flow is greatest in the central streams because of the relatively high flow velocities (4). The impact and sudden deflection of central streams at the apex result in the transmission of a pulsatile impulse to that region of a bifurcation, which does not occur elsewhere in the vessel. Moreover, the peak force of the impulse is great because of the brief impact time (impulse equals the change in momentum, and may be expressed as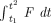 
where F is the net force producing the change in momentum, and dt is the time of impact). For a given change in momentum, a short impact time will result in the transmission of a high force. At the moment of impact, the kinetic energy of the moving blood is converted to pressure energy (stagnation pressure) at the apex. Other areas of the vessel wall are not subjected to this “extra” pressure. The total pressure acting at the apex equals the sum of the transmural pressure and the stagnation pressure. This concept was demonstrated first in models by Forbus (5).
In this article, we investigate computationally the high pressure and shear stresses, previously demonstrated, arising at both curved arterial segments and arterial bifurcations, and study their relationship to aneurysm formation and growth.
Methods
The assumptions and two-dimensional model equations previously presented (3) in detail are reviewed briefly here.
Assumptions:
The fluid (blood) is incompressible (ie, Newtonian).
The flow is laminar and isothermal.
The artery is rigid.
Equations
Conservation of Momentum
Conservation of Mass (Continuity)
Boundary Conditions
where a is a dimensionless scaling constant, p is pressure, ui and uj are the components of the velocity vector, and fi is an external force vector.
As with the straight arterial model presented in (3), we employed the quasi-Newtonian, Broyden's update method as the solution scheme for these models, and the Jacobian matrix was reformed at all five iterations. This method proved to be very efficient, with most time steps converging in, at most, three iterations. Similarly, the trapezoid rule with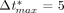 
was used for the time integration in the transient analysis.
Results
We present the simulation results for the problem of two-dimensional, isothermal, Newtonian flow in a curved (90°) arterial segment and an arterial bifurcation. The time-varying forcing function is supplied by an oscillatory pressure gradient described in (3). In all cases, for reasons previously described (3), the mesh is graded so that the intraelement lengths decrease in the direction of the arterial walls. This meshing strategy is used for all the models reported in this article.
Curved Arterial Segment Model
Lateral aneurysm formation in cerebral arteries was explored using a simulation analysis on a curved arterial segment with three differently sized aneurysms.
Stage 1: Curved Artery with Aneurysm Bleb
We modified the finite element mesh to reflect the presence of an aneurysm bleb in the location indicated in previous simulations (3) as having the highest wall pressures. The finite element mesh used in this model consisted of 609 quadrilateral nodal elements.
The local flow field is shown in Figures 1A and B. Initially the fluid particles are aligned across the lumen at the location of the proximal aneurysm neck. It can be seen that the flow impinges on the distal aneurysm neck, and the fluid enters the local dilatation at this site. After circulating through the bleb, the outer fluid particles are entrained by the main arterial flow, and carried downstream. Notice that there is separation of flow from the outer (lateral) wall in the bend region and a small local recirculation region within the bleb itself. A counterclockwise rotating vortex is present within the aneurysm bleb during both the acceleration and deceleration portions of systole. The degree of flow separation and recirculation is greater during systolic deceleration than during acceleration.
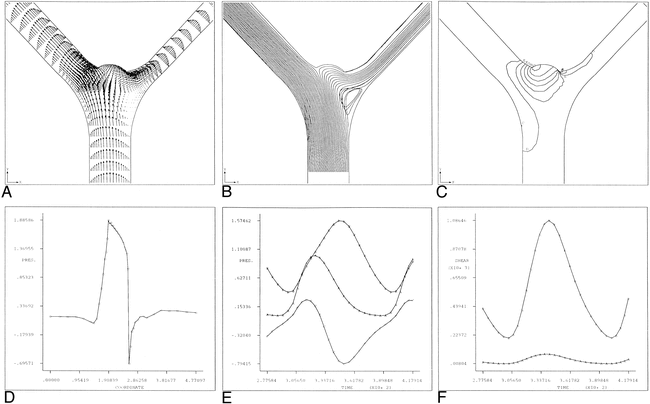
Curved artery with aneurysm bleb.
A, Instantaneous velocity vector plot of flow in curved arterial segment with aneurysm bleb during deceleration portion of systole.
B, Streamline contour plot for curved arterial segment model with aneurysm bleb during deceleration portion of systole (t* = 245). Flow separation along the lateral wall and a zone of local recirculation are evident. The extent of both separation and recirculation is greatest during the deceleration portion of systole.
C, Instantaneous pressures during deceleration portion of systole for curved arterial model with aneurysm bleb. Shown are pressure contours at t* = 245 and the corresponding line graph of the pressure along the outer (lateral) wall from the inlet (i) to the outlet (o). Note that the pressure is fairly constant along the body of the aneurysm, with the highest pressure occurring at the distal neck site. For reference purposes, contour A corresponds to a value of −0.362 dpu (dimensionless pressure units) whereas contour O corresponds to a value of 0.555 dpu.
D, Pressure history plot for curved arterial model with aneurysm bleb showing pressure at proximal and distal aneurysm necks over one cardiac cycle. Curve A corresponds to the segment inlet, Curve B corresponds to the proximal aneurysm neck site and Curve C corresponds to the distal neck site.
E, Time history plot of shear rates at proximal and distal aneurysm necks. Curves A and B correspond to the proximal and distal neck sites, respectively. Note that the shear rate values at the distal neck exceed those of the proximal neck throughout the entire cardiac cycle.
Figure 1C shows the pressures that develop along the lateral (outer) wall during the deceleration portion of systole. Figure 1D shows the time history plot of the pressure at the proximal and distal aneurysm bleb neck sites. Notice that the pressure at the distal neck exceeds that of the proximal neck.
In addition to the expected local pressure increase at the bend, the simulation results show a secondary pressure increase at the distal (downstream) aneurysm neck. This phenomenon is especially evident during the deceleration portion of cardiac systole. Furthermore, if the local shear rates at both the proximal and distal aneurysm necks are considered, it can be seen that the values at the distal neck are appreciably greater than those at the proximal neck, especially during systolic deceleration (Figure 1E). This indicates that the distal aneurysm neck is subjected to greater hemodynamic stress than its proximal counterpart.
These results correlate well with the surgical observations that most intracranial aneurysms of this type tend to “lean” in the direction of flow. It is postulated that this is caused by the distal (downstream) portion of the aneurysm being subjected to greater mechanical strains than the proximal (upstream) portion. Consequently, aneurysm growth proceeds primarily from the distal aneurysm neck, and progresses in the direction of the arterial blood flow.
Stage 2: Curved Artery with Saccular Aneurysm
The same boundary and initial conditions were used here as in the previous simulation; however, the finite element mesh was modified based on the results obtained from the aneurysm bleb simulation, with the enlarged aneurysm leading in the direction of flow.
Again the results are presented for the dimensionless time (t* = 245), which corresponds to the deceleration portion, because it is at this time that the pressures and stresses at the apex of the bifurcation are maximal.
As the blood travels through the main lumen of the artery, it impinges on the distal aneurysm neck. The impinged flow is then diverted into the aneurysm sac at the site of the distal neck. Within the aneurysm, the blood recirculates, and travels in a direction retrograde to the flow in the main arterial lumen. Although the intra-aneurysmal flow velocities are small in magnitude, the blood continues to recirculate within the aneurysm until it is entrained into the mainstream flow, and carried downstream. The flow field is shown in Figure 2A, whereas Figure 2B shows the continuous particle paths.
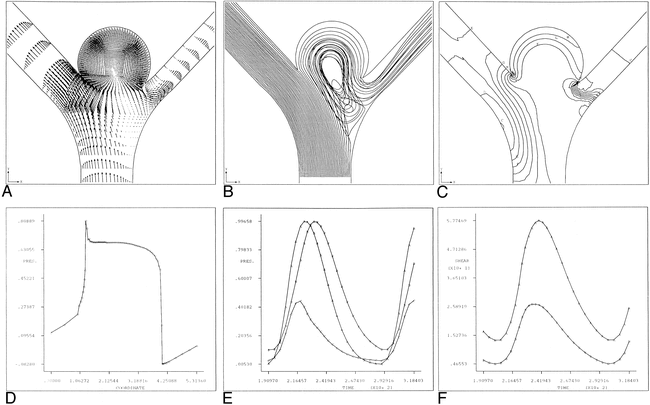
Curved artery with saccular aneurysm.
A, Instantaneous velocity vector plot of flow in curved arterial segment with saccular aneurysm during deceleration portion of systole.
B, Continuous particle paths for t* = 200–400 for fully developed saccular aneurysm model. Initially the particles were aligned across the main lumen at the location of the proximal aneurysm neck.
C, Instantaneous pressure contours during deceleration portion of systole for the curved arterial model with a fully developed aneurysm. Shown here are pressure contours at dimensionless time, t* = 245. Here, contour A corresponds to a value of 0.531 dpu (dimensionless pressure units) while contour M corresponds to a value of 0.563 dpu.
D, Pressure history plot for curved arterial segment model with saccular aneurysm showing pressure at proximal and distal aneurysm necks over one cardiac cycle. Curve A corresponds to the segment inlet, Curve B corresponds to the proximal aneurysm neck site (node 851) and Curve C corresponds to the distal neck site (node 1251).
E, Time history plot of shear rates at proximal and distal aneurysm necks. Curve A and B correspond to the proximal (node 851) and distal (node 1251) neck sites, respectively. Note that the shear rate values at the distal neck exceed those of the proximal neck throughout the entire cardiac cycle.
Although the aneurysm vortex is present throughout the entire cardiac cycle, its magnitude is the greatest during the deceleration phase. This may be attributed to the fact that during the acceleration portion of systole, the increasing pressure within the aneurysm sac inhibits fluid motion. After there is a sufficient reduction in the magnitude of the intra-aneurysmal pressure, there is less resistance to fluid motion and the strength of the vortex increases during the beginning of systolic deceleration. Toward the end of the deceleration portion of systole, the intra-aneurysmal flow decreases until the next systole. Figure 2C shows the pressures that develop during systolic deceleration, and Figure 2D shows the time history plot of the pressure at the proximal and distal aneurysm necks. The shear rates at the proximal and distal aneurysm necks are shown in Figure 2E.
Figure 2C reveals some interesting information about the pressures in the vicinity of the aneurysm. As in the previous model, there is a local pressure increase present at the bend. Nonetheless, unlike the previous model, this model does not display the secondary pressure increase at the site of the distal neck. Rather, the pressure remains fairly constant along the entire length of the aneurysm wall. The small variations in intra-aneurysmal pressure also can be seen in this figure. It can also be seen that within the aneurysm itself, the higher pressures exist distally and appear to “push” the aneurysm in the predicted direction of growth. Figure 2E clearly illustrates that the distal neck is subjected to greater shear throughout the cardiac cycle. This, together with the pressure information, undoubtedly suggests that the distal aneurysm neck is subjected to greater hemodynamic stress than any other region in the arterial segment.
Arterial Bifurcation Model
Because the majority of intracranial aneurysms occur at bifurcations, this model is of paramount importance for understanding the hemodynamic factors that are responsible for aneurysm development.
The results of our observations for a normal arterial bifurcation model without an aneurysm demonstrate that a stagnation point exists at the apex of the bifurcation (3). This localized region of low flow results in high impact pressures at the apex. In fact, the maximal pressure generated at the apex of the bifurcation is more than twice the maximal luminal pressure in the parent artery (3). We hypothesize that this local region of high stress is primarily responsible for aneurysm formation at the arterial bifurcations. Based on the results shown in (3), the original finite element mesh was modified to account for the presence of an aneurysm bleb, thus beginning aneurysm formation. The results for three distinct stages of aneurysm development are given in the following subsections.
Stage 1: Arterial Bifurcation with Aneurysm Bleb
We modified the previous arterial bifurcation to account for the presence of a saccular aneurysm in the initial stages of development.
Figures 3A–B depict the resultant flow field and particle paths that arise during the deceleration portion of cardiac systole. Initially, the fluid particles are aligned across the lumen of the parent artery proximal to the bifurcation. It can be seen that the flow impinges on the bleb neck on the side of the larger daughter vessel. A stagnation point is present along the dome of the bleb itself. After impacting the dome, the fluid particles are diverted laterally and carried down each daughter branch. Figure 3B clearly illustrates that the bulk of the flow entering the bifurcation from the parent vessel is diverting into the dominant daughter branch. For future reference, the aneurysm neck on the side of the larger daughter branch will be called N1, and the neck on the side of the smaller daughter branch will be called N2.
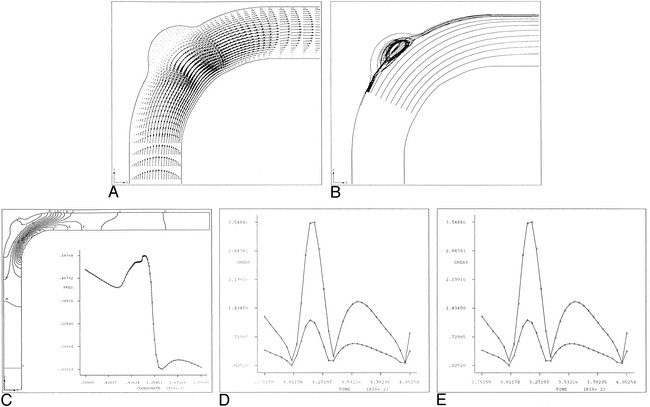
Arterial bifurcation with aneurysm bleb.
A, Instantaneous velocity vector plot of flow in arterial bifurcation model with aneurysm bleb during deceleration portion of systole.
B, Continuous particle paths for t* = 200–400 for arterial bifurcation model with aneurysm bleb. Initially the particles were aligned across the lumen of the parent artery proximal to the bifurcation.
C, Instantaneous pressure contours for arterial bifurcation model with aneurysm bleb during deceleration portion of cardiac systole (t* = 245). Plot corresponds to time of maximal pressure at bifurcation. For reference purposes, contour A corresponds to a value of -0.567 dpu (dimensionless pressure units) whereas contour J corresponds to a value of 1.757 dpu.
D, Line plot of instantaneous pressure along arterial wall corresponding to figure 3E. Location of maximal pressure corresponds to location of stagnation point at aneurysm neck site N1.
E, Pressure time history plot for asymmetrical arterial bifurcation model with aneurysm bleb over one cardiac cycle. Curve A corresponds to the vessel inlet, Curve B corresponds to the aneurysm neck site N1 and Curve C corresponds to the aneurysm neck site N2.
F, Time history plot of shear rates for asymmetric arterial bifurcation model with aneurysm bleb at aneurysm neck sites N1 and N2. Curve A and B correspond to aneurysm neck sites N1 and N2, respectively. Note that the shear rate values at N2 exceed those of N1 throughout the entire cardiac cycle.
The instantaneous pressure contour plots and corresponding line graphs are shown in Figures 3C–D. As we noted previously, high-impact pressures develop at the stagnation point. It can be seen that the point of highest impact pressure occurs near the aneurysm neck on the side of the larger daughter branch. At this point, the maximal pressure is 89% higher than the peak luminal pressure in the parent (feeding) artery. Figure 3E shows the time history plot for the pressures at the inlet, the aneurysm bleb neck N1, and the neck N2. Figure 3F shows the shear rate as a function of time at N1 and N2 over one entire cardiac cycle. From this figure, it is clear that the shear rates at N2 greatly exceed those at N1. This result has some interesting implications. Whereas the highest pressure is found at the aneurysm neck N1, it is at N2 that the greatest shear rates are found. Therefore, both aneurysm necks are subjected to high states of hemodynamic stress: stress at N1 owing to pressure and at N2 owing to shear. It is logical to predict that aneurysm growth will progress with mouth widening.
Stage 2: Arterial Bifurcation with Saccular Aneurysm
Figures 4A–B depict the resultant flow field, particle paths, and streamlines that arise during the deceleration portion of cardiac systole for a fully developed saccular aneurysm at the apex of the bifurcation.
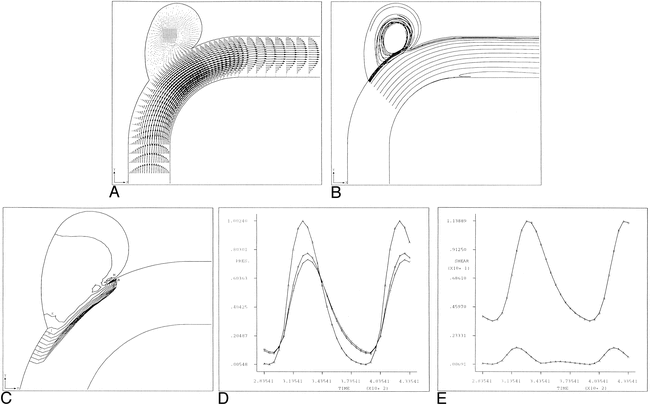
Arterial bifurcation with saccular aneurysm.
A, Instantaneous velocity vector plot of flow in arterial bifurcation model with saccular aneurysm during deceleration portion of systole.
B, Continuous particle paths for t* = 200–400 for arterial bifurcation model with saccular aneurysm. Initially the particles were aligned across the lumen of the parent artery.
C, Instantaneous pressure contours for arterial bifurcation model with saccular aneurysm during deceleration portion of cardiac systole (t* = 245). Plot corresponds to time of maximal pressure at bifurcation. For reference purposes, contour A corresponds to a value of -0.308 dpu (dimensionless pressure units) whereas contour O corresponds to a value of 1.535 dpu.
D, Line plot of instantaneous pressure along arterial wall corresponding to figure 4C. Shown is the pressure along arterial wall and aneurysm dome from node 2189 to node 2231. Location of maximal pressure corresponds to location of stagnation point at aneurysm neck site N1.
E, Pressure time history plot for arterial bifurcation model with saccular aneurysm over one cardiac cycle. Curve A corresponds to the vessel inlet, Curve B corresponds to the aneurysm neck site N1 and Curve C corresponds to the aneurysm neck site N2. Note the secondary rise in pressure at the neck N2. This pressure oscillation may give rise to vibrations at the neck site and further increase the chance of structural fatigue.
F, Time history plot of shear rates for arterial bifurcation model with saccular aneurysm at aneurysm necks sites N1 and N2. Curves A and B correspond to aneurysm neck sites N1 and N2, respectively. Note that the shear rate values at N2 exceed those of N1 throughout the entire cardiac cycle.
Initially, the fluid particles are aligned across the lumen of the parent artery proximal to the bifurcation. During the deceleration portion of systole, the flow enters the aneurysm on the side of N1, and exits on the side of N2, but counterclockwise rotating vortices also exist, both within the aneurysm and main feeding artery. The intra-aneurysmal vortex only occurs after the pressure within the aneurysm has dropped enough such that fluid motion is not prevented. Virtually all the fluid that perfuses the narrower arterial branch has either first circulated through the aneurysm or has been involved in the intra-aneurysmal vortex.
The instantaneous pressure contour plots and corresponding line graphs are shown in Figures 4C–D. These figures illustrate that there is a stress concentration in the immediate vicinity of the aneurysm. During the deceleration portion of systole, the pressures are highest at the aneurysm neck N1. At this location the maximal pressure is 60% greater than the peak luminal pressure in the parent artery. In this situation, the pressure along the dome of the aneurysm is fairly constant at any given time. Figure 4E shows the pressure time history plot at three important locations: the inlet, the aneurysm neck N1, and the aneurysm neck N2.
One point of interest is the secondary rise in pressure that occurs at the neck N2 midway into the deceleration portion of systole (Fig 4E). We believe that this pressure oscillation is a result of the counterclockwise rotating vortex that develops during systolic deceleration. This pressure oscillation may give rise to vibrations at the neck site, and further increase the chance of structural fatigue. Figure 4F shows the shear rate as a function of time at N1 and N2 over one entire cardiac cycle. From this figure, it is clear that the shear rates at N2 again greatly exceed those at N1. Another point of interest is the shape of the shear rate plot. The shear rate at the aneurysm neck N1 displays a sharper peak at its maximal value. The rapid increase and decrease in shear rate at the aneurysm neck N2 may act more like an impulse-producing structural fatigue.
Stage 3: Arterial Bifurcation with Wide-Mouthed Saccular Aneurysm
Figures 5A–B show the resultant flow fields and particle paths that arise during deceleration portions of cardiac systole. Initially, the fluid particles are aligned across the lumen of the parent artery proximal to the bifurcation. During both the acceleration and deceleration portions of systole, the flow enters the aneurysm on the side of N1. In this geometric configuration, the entire aneurysm is flushed with every heartbeat. After circulating through the body of the aneurysm, the blood exits on the side of N2, and proceeds down the smaller daughter branch. Virtually all the fluid that perfuses the smaller daughter branch has circulated first through the aneurysm. For the case of the wide-mouthed saccular aneurysm, the intra-aneurysmal flow is sufficient to perfuse the aneurysm sac fully with each cardiac cycle, thus reducing the chance of clot formation within the aneurysm.
Arterial bifurcation with wide-mouthed saccular aneurysm.
A, Instantaneous velocity vector plot of flow in arterial bifurcation model with wide-mouthed saccular aneurysm during deceleration portion of systole.
B, Continuous particle paths for t* = 200–400 for arterial bifurcation model with wide-mouthed saccular aneurysm. Initially the particles were aligned across the lumen of the parent artery.
C, Instantaneous pressure contours for arterial bifurcation model with wide-mouthed saccular aneurysm during deceleration portion of cardiac systole (t* = 245). Plot corresponds to time of maximal pressure at bifurcation. For reference purposes, contour A corresponds to a value of -0.135 dpu (dimensionless pressure units), whereas contour O corresponds to a value of 0.776 dpu.
D, Line plot of instantaneous pressure along arterial wall corresponding to figure 5C. Location of maximal pressure corresponds to location of stagnation point at aneurysm neck site N1.
E, Pressure time history plot for arterial bifurcation with wide-mouthed edsaccular aneurysm over one cardiac cycle. Curve A corresponds to the vessel inlet, Curve B corresponds to the aneurysm neck site N1, and Curve C corresponds to the aneurysm neck site N2.
F, Time history plot of shear rates for arterial bifurcation with wide-mouthed saccular aneurysm at aneurysm necks site N1 and N2. Curves A and B correspond to aneurysm neck sites N1 and N2, respectively. Note that the shear rate values at N1 exceed those of N2 throughout the entire cardiac cycle.
The instantaneous pressure contour plots and corresponding line graphs are shown in Figures 5C–D. In the wide-mouthed aneurysm configuration, the maximal pressure in the vicinity of the aneurysm is 20% less than the peak luminal pressure in the parent artery. Figure 5E shows the time history plot of the pressure at the segment inlet, the aneurysm neck N1, and the neck N2. Figure 5F shows the shear rate as a function of time at N1 and N2 over one entire cardiac cycle. From this figure, it is clear that the shear rates at N2 greatly exceed those at N1. In this stage, as in the previous ones for this case, we see that the highest pressure is at the neck N1, whereas the highest shear rates are at N2. Nonetheless, it should be noted that these pressures and shear rates are decreasing as a function of neck diameter.
Discussion
We have presented a comprehensive analysis of fluid flow in curved arteries and arterial bifurcations and the relationship of these hemodynamics to aneurysm formation and growth. The two-dimensional Navier-Stokes equations governing pulsatile Newtonian flow were solved using the finite element method (3). These studies were limited to the case of rigid vessel walls, which we believe is an acceptable simplification for local flow investigations, because intracranial arteries and their associated aneurysms are less distensible than normal extracranial arteries (6–9). Moreover, previous investigators have compared results of flow simulations in both rigid and compliant tubes, and concluded that there are few appreciable differences between the two assumptions (10–13). A Reynolds' number of Re=750 was used in all the studies, which corresponds to the average Reynolds' number in the intracranial arteries under normal physiologic conditions as computed from transcranial Doppler data. These models show the essential flow phenomena except for the effects of secondary motion.
Based on the results for the flow and pressure fields in the normal arterial segment models, it is possible to predict the location of aneurysm development and modify the finite element mesh accordingly to account for the presence of an aneurysm in its initial stage of development (bleb phase). For the case of the curved arterial segment model, high pressures arise at the apex of the bend along the outer (lateral) arterial wall, whereas for the bifurcation case, high pressure exists at the apex of the bifurcation.
The progressive formation of saccular aneurysms on curved nonbifurcating arteries were investigated, and revealed a number of suspected but unproved hypotheses concerning mechanisms that play a significant role in the origin of aneurysms. A local pressure increase is present along the lateral (outer) wall in the region of the bend. This localized zone of high pressure, and thus high hemodynamic stress, appears to be responsible for the occurrence of these saccular aneurysms on the lateral wall of curved arteries. We theorize that once the yield stress of the arterial wall is exceeded, the wall undergoes plastic deformation, and an aneurysm bleb develops. When a small aneurysm develops, the distal neck is the primary target of hemodynamic stress because the blood impinges on the wall throughout the entire cardiac cycle. Within the aneurysm bleb, high pressures and shear rates at the distal neck cause the dilatation to progress at this site, resulting in a fully developed saccular aneurysm that leans in the downstream direction. Thus, the major changes in hemodynamics, as well as aneurysm growth, occur at the neck and not in the dome of aneurysms, as anecdotally suspected. These results indicate that the aneurysm mouth will enlarge as the distal neck site is pushed downstream. In addition, because there is little flow within the narrow-mouthed aneurysm, there is a high propensity for thrombus formation. The simulation was repeated for a wider-mouthed aneurysm. In these cases, as aneurysm neck growth proceeds, the intra-aneurysmal pressures begin to decrease, possibly representing a compensatory mechanism to reduce the risk of aneurysmal wall stress and rupture. In contrast, the degree of intra-aneurysmal flow is increased in comparison to the narrow-mouthed aneurysm model, suggesting less of a chance for intra-aneurysmal thrombus formation.
The second major class of arterial geometries investigated was that of an asymmetric arterial bifurcation. This vascular geometry is of special interest because intracranial aneurysms most commonly occur at bifurcations of the circle of Willis. Initially, pulsatile flow in an arterial bifurcation without an aneurysm was simulated (3). The results indicated that owing to the presence of high pressures and shear rates, aneurysm formation is likely to occur at the apex of the bifurcation. As with the curved artery model, the finite element mesh was modified to account for the presence of an aneurysm bleb at the apex of the bifurcation. The simulation results suggest that the aneurysm neck on the side of the larger daughter branch is the site of high-impact pressures, and these pressures are almost twice the luminal pressure in the parent artery. This result suggests that pressure measurements routinely obtained may underestimate dramatically pressure in the vicinity of an aneurysm. On the other hand, the aneurysm neck on the side of the smaller daughter branch is the location of the highest shear rates. Therefore, both sides of the aneurysm neck are subjected to increased states of hemodynamic stress, one arising from pressure, and the other from shear.
We then modified the model to investigate a more fully developed saccular aneurysm. The results of this simulation are of particular interest. It was shown that a weak counterclockwise rotating vortex is established in the aneurysm sac during the deceleration portion of systole. In addition, all the fluid that circulates through the aneurysm itself proceeds down the smaller daughter branch, and virtually all the fluid that flows down the smaller branch circulates through the aneurysm. There is little flow deep within the dome of the narrow-mouthed saccular aneurysm, indicating an increased chance for intra-aneurysmal thrombus formation. The fact that high hemodynamic stresses are exhibited at the aneurysm necks, suggests a tendency for the size of the aneurysm mouth to increase. For the narrow-mouthed aneurysm configuration, the maximal pressure in the vicinity of the aneurysm is up to 2.5 times higher than that of the peak luminal pressure in the parent artery.
Finally, the computational results for a wide-mouthed saccular aneurysm again indicated the presence of high pressures at the aneurysm neck on the side of the dominant daughter branch and high shear rates at the proximal neck site. In contrast to the narrow-mouthed aneurysm model, the amount of intra-aneurysmal flow is dramatically increased. This finding further supports the hypothesis that wide-mouthed aneurysms are less susceptible to thrombus formation. Furthermore, it also indicates that endovascular coil placement may be inappropriate for the case of wide-mouthed aneurysms, as conditions exist that may result in the coil being washed out of the aneurysm and carried downstream.
It has been reported (14) that mechanical deformation of the vessel wall and high shear stresses are responsible for the local release of the endothelial-derived relaxation factor (EDRF) protein, which is thought to be nitrous oxide. It is likely that EDRF plays some role in the evolution of saccular aneurysms. The results presented in this paper suggest that, in the absence of any underlying disease, the aneurysmal process is a mechanically mediated event (ie, a mechanical deformation in response to high stress (pressure and shear) regardless of the action of EDRF. We have demonstrated clearly that high pressures and shear rates exist at the sites common to aneurysm formation. The high shearing forces may result in damage to the endothelial cells lining the artery, weakening the site structurally. In response to shear-induced EDRF release, the vessel wall is relaxed locally, making it even more susceptible to pressure-induced deformation. In this manner, EDRF may in essence exert a positive feedback mechanism that facilitates aneurysm formation.
Acknowledgments
This research was partially funded by support from the Hearst Foundation and the Hewlett Packard Corporation.
Footnotes
1 Address reprint requests to Robert J. Sclabassi, M.D., Ph.D, Presbyterian-University Hospital, Suite B-400, 200 Lothrop Street, Pittsburgh, PA 15213-2582.
References
- Received August 21, 1998.
- Accepted after revision February 11, 1999.
- Copyright © American Society of Neuroradiology
In this issue
Jump to section
Related Articles
Cited By...
- Bifurcation geometry remodelling of vessels in de novo and growing intracranial aneurysms: a multicenter study
- Bifurcation geometry remodelling of vessels in de novo and growing intracranial aneurysms: a multicenter study
- Loss of Vascular Myogenic Tone in miR-143/145 Knockout Mice Is Associated With Hypertension-Induced Vascular Lesions in Small Mesenteric Arteries
- Low prevalence of fetal-type posterior cerebral artery in patients with basilar tip aneurysms
- Risk Factors Associated With the Presence of Unruptured Intracranial Aneurysms
- High curvature of the internal carotid artery is associated with the presence of intracranial aneurysms
- High WSS or Low WSS? Complex Interactions of Hemodynamics with Intracranial Aneurysm Initiation, Growth, and Rupture: Toward a Unifying Hypothesis
- A retrospective analysis on the natural history of incidental small paraclinoid unruptured aneurysm
- The Effect of Intracranial Stent Implantation on the Curvature of the Cerebrovasculature
- The role of circle of Willis anomalies in cerebral aneurysm rupture
- Risk Analysis of Unruptured Aneurysms Using Computational Fluid Dynamics Technology: Preliminary Results
- Hemodynamics of Cerebral Aneurysm Initiation: The Role of Wall Shear Stress and Spatial Wall Shear Stress Gradient
- Treatment of Intracranial Aneurysms by Functional Reconstruction of the Parent Artery: The Budapest Experience with the Pipeline Embolization Device
- Involvement of Mitogen-Activated Protein Kinase Signaling in Growth and Rupture of Human Intracranial Aneurysms
- Configuration of intracranial arteries and development of aneurysms: A follow-up study
- Role of the Bloodstream Impacting Force and the Local Pressure Elevation in the Rupture of Cerebral Aneurysms
- Hemodynamic Analysis of an Adult Vein of Galen Aneurysm Malformation by Use of 3D Image-Based Computational Fluid Dynamics
- The Promise of Computational Fluid Dynamics As a Tool for Delineating Therapeutic Options in the Treatment of Aneurysms
- In Vitro Measurement of Fluid-Induced Wall Shear Stress in Unruptured Cerebral Aneurysms Harboring Blebs